Predictive value of lactate in unselected critically ill patients: an analysis using fractional polynomials
Introduction
Lactate is the metabolic product of anaerobic glycolysis. In situations of low oxygen supply or tissue hypoxia, pyruvate will no longer enter into mitochondria for aerobic metabolism but will be reduced to lactate, leading to increases in arterial blood lactate concentrations (1,2). However, hyperlactatemia is not necessarily associated with hypoxia. There are varieties of medications that have been linked to hyperlactatemia, such as nucleoside reverse transcriptase inhibitors, metformin, epinephrine and methanol (3,4). Lactate can be produced from all kinds of tissues, including skeletal muscle, brain, red blood cell and intestine. Critically illness is often associated with increased production of in lactate from lung, blood cells and splanchnic organs. On the other hand, because lactate is primarily cleared via liver and kidney, dysfunction of these organs during critical illness also contribute to the elevated lactate levels (5).
Due to the high prevalence of hyperlactatemia in critically ill patients, its association with clinical outcome has been extensively studied over the past two decades (6). In the early 1990s, Abramson D and coworkers demonstrated that lactate levels were strongly associated with survival in a cohort study involving 27 patients (7). Thereafter, investigations on the association of lactate or lactate clearance with clinical outcome increase exponentially (8-10). Higher lactate value is consistently associated with adverse clinical outcomes and rapid lactate clearance after treatment is associated with improved outcomes. However, most of these studies are observational studies which, whether it is prospective or retrospective, are subject to confounding bias. As a result, these studies have employed multivariable regression analysis by assuming that the effect of lactate on mortality or other clinical outcomes were linear. Furthermore, these studies were limited in that they predefined a certain time point for lactate clearance, and the times varied across studies, making it difficult for clinicians to determine when lactate should be rechecked. In the current study, fractional polynomial Cox proportional hazards model were fitted to investigate the association of lactate levels and mortality. This model allows for more flexibility in the shape of the curve. Secondly, we will investigate how normalization time impacts the clinical outcome.
Methods
Database
Our study was an analysis of a large clinical database named Multiparameter Intelligent Monitoring in Intensive Care II (MIMIC-II, http://physionet.org/mimic2) (11). This database is a research archive of data collected from patients in intensive care unit (ICU) and is freely accessible for the public. The data contained in MIMIC-II was collected at the ICUs of Beth Israel Deaconess Medical center in Boston from 2001 to 2008. The following data were available: demographics, laboratory test, vital sign recording, fluid and medical records. The establishment of MIMIC-II database was approved by the Institutional Review Boards of the Massachusetts Institute of Technology (Cambridge, MA, USA) and the Beth Israel Deaconess Medical Center. The patient records/information was anonymized and de-identified prior to analysis, and informed consent was not obtained from each participants. The database was continuously updated with the latest version of 2.6 that contained records from over 32,000 subjects. Our access to the database was approved after completing the NIH web-based training course “Protecting Human Research Participants” by the author Z.Z. (Certification Number: 1132877). Data acquisition was completed by using Structural Query Language (12).
Study population
All patients contained in MIMIC-II clinical database were potentially eligible for the present analysis. Adult patients with initial arterial blood lactate >2 mmol/L were included. Exclusion criteria included: (I) neonates; and (II) patients with missing data on arterial blood lactate.
Data abstraction and management
Data on following aspects were extracted: age, gender, SAPSI-1, sequential organ failure assessment (SOFA), admission type (elective, emergency and urgent), comorbidities (congestive heart failure, paralysis, chronic pulmonary disease, complicated diabetes, renal failure, metastatic cancer), date of ICU admission, date of death, ICU mortality and hospital mortality. In order to protect health information of individual patients, the database had obscured real ages for those aged over 90 years. All of them appeared to be 200 years old on first admission. The median age for these patients was 91.4 and we use it as a surrogate age for them. For patients who discharged alive, we obtained the date of death from the Social Security Death Index (SSDI) to determine out-of-hospital mortality. All measurements of arterial blood lactate and associated time were obtained. Lactate normalization was achieved when there was at least one measurement of lactate dropped below 2 mmol/L. Normalization time was the time interval between ICU admission and the time point when lactate normalization occurred.
Statistical analysis
Data were expressed as mean and standard error, or median and interquartile range as appropriate. Variables were compared between patients with and without lactate normalization with univariate analysis. Data of normal distribution were compared using t test and skewed data were compared using Wilcoxon rank-sum test. 28-day mortality was used as the primary end point and variables were compared between survivors and non-survivors.
The Cox proportional model was built by using purposeful selection of covariates. Variables with P<0.2 in bivariate analysis and those considered to be clinically relevant were included to establish the initial multivariable model. The later included the severity scores and age. Variables in the initial model would be deleted if P>0.1 from the Wald test. If the removed covariate produced a significant change (>20% change) in the coefficient of lactate, it was thought to be a confounder and would be remained in the model. Any variable excluded should be added back to the model to confirm that it was neither statistically significant nor an important confounder. The process continued until no covariate could be deleted, and the preliminary main effects model had been built up to this point (13). To overcome the obstacle in model building that the relationship between outcome and predictor might be non-linear, the next step was to determine the scale of lactate by using fractional polynomials (14,15). We first determined the best fitting fractional polynomial regression model of second-degree (FP2) by choosing power transformations from the set –2, –1, –0.5, 0, 0.5, 1, 2, 3, where 0 denoted the log transformation. The best fitting model was determined using a deviance difference test. With closed test procedure (15), the deviance of FP2 was compared to deviances of the function with omitted variable, linear function and FP1. Statistical significance of the deviance difference was tested by using χ2 test. Statistical analyses were performed using software package Stata 12.0 (College Station, Texas 77845 USA). Conventional P<0.05 was considered to be statistically significant.
Results
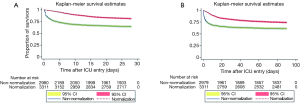
A total of 6,291 patients were identified to be eligible for the present study, including 3,311 patients with lactate normalization and 2,980 of non-normalization (Table 1). There were no statistically significant differences between normalization and non-normalization groups in age, gender, comorbidities of paralysis, chronic pulmonary disease, complicated diabetes and renal failure. Non-normalization was associated with significantly increased risk of death irrespective of the time frame for the definition of mortality: 28-day mortality (35.50% vs. 18.63%; P<0.001), 90-day mortality (38.83% vs. 25.79%; P<0.001), ICU mortality (23.06% vs. 13.24%; P<0.001) and hospital mortality (31.44% vs. 18.77%; P<0.001). Figure 1 displays the Kaplan-Meier survival curves for 28- and 90-day mortality. The result showed that lactate normalization was associated with significantly longer survival time.
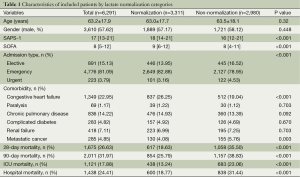
Full table
Among the 6,291 included patients, there were 1,675 non-survivors and 4,616 survivors within 28 days (Table 2; overall mortality rate: 26.6%). Non-survivors appeared to be older (67.9±16.9 vs. 61.5±17.9; P<0.001), had higher first SAPS-I (20 vs. 16; P<0.001) and SOFA scores (11 vs. 8; P<0.001). Patients admitted to ICU electively were more likely to survive (18.71% vs. 4.46%; P<0.001), whereas those admitted emergently were more likely to die (91.15% vs. 77.70%; P<0.001). With respect to comorbidities, patients with congestive heart failure (27.53% vs. 21.42%; P<0.001), renal failure (10.64% vs. 5.93%; P<0.001), weight loss (4.68% vs. 3.13%; P=0.005) and metastatic cancer (9.02% vs. 3.45%; P<0.001) were more likely to die within 28 days.
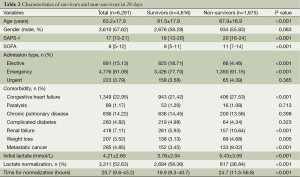
Full table
All variables with P<0.2 were entered into proportional hazard model for covariate selection. Two models were established: one included initial lactate (L0) and the other included the time for lactate normalization (T). Fractional polynomials of second degree were applied. After model fitting, the best powers of L0 among 44 models were -2 and -1 with the deviance of 19,944.51 (Table 3). The FP2 model significantly improved model fit relative to that without L0 in the model (Deviance Difference =76.1, P value <0.001), the linear model (Deviance Difference =11.2, P value =0.011) and the FP1 model with the power of 0.5 (Deviance Difference =10.5, P value =0.005). The best powers of T among 44 models were 0.5 and 3 with the deviance of 7,965.63. The FP2 model significantly improved model fit relative to that without T in the model (Deviance Difference =17.9, P value =0.001), the linear model (Deviance Difference =16.0, P value =0.001) and the FP1 model with the power of 0 (Deviance Difference =6.6, P value =0.037). Figure 2 displays the fractional polynomial functions adjusted for covariates. The results showed that the hazard increased with the increase in initial lactate level. The slope was most steep from 3 to 8 mmol/L, and after 10 mmol/L the slope tempered. With respect to the normalization time, the hazard increased with increases in normalization time before 150 hours, after that the hazard begin to decrease but with wide uncertainty as reflected by the wide 95% confidence interval.
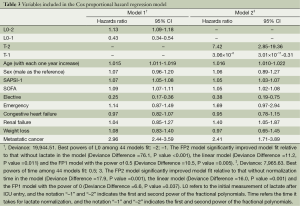
Full table
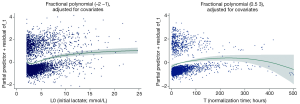
Figure 3 displays contour plot showing the relationship between normalization time, initial lactate and mortality stratified by quartiles of SOFA score. The results showed that while the higher initial lactate was consistently associated with higher mortality, longer normalization time appeared to be associated with higher mortality in patients with SOFA >12.

Discussion
The study showed that both initial lactate and normalization time were significantly associated with increased risk of death in ICU patients. Higher initial lactate and longer normalization time were associated with increased hazard of mortality. Commonly employed normalization time for predicting mortality ranged from 6 to 72 hours in literatures (7,9,16,17), because any prolongation of the time frame may be irrelevant for both risk stratification and resuscitation guidance. In our study we showed that normalization time within 100 hours was positively associated with the hazard.
Our study confirmed previous finding that initial lactate was able to predict clinical outcome (18). In patients underwent cardiothoracic surgery, Maarslet and colleagues (19) found that an increased initial lactate >4.5 mmol/L resulted in an odds ratio of 8.4 (95% CI: 1.5-46.1) for mortality. Lactate level measured at 6 hours after ICU admission was also found to be an independent predictor of complications after major cardiothoracic surgery (20). Some investigators have compared the predictive value of lactate to complex physiological scores in a cohort of cardiothoracic surgery patients. They found that the diagnostic performance of lactate was significantly superior to these scores, as reflected by an area under curve (AUC) of 0.88 for lactate versus 0.83, 0.79 and 0.76 for SOFA, SAPS II and APACHE II, respectively (21). However, these studies used mortality as a binary outcome and ignored the survival time, which may be biased in situations such as when both groups have the same mortality rate but the time to death is significantly different. Furthermore, that study is limited by the small sample size and the percentage of patients with the target event death was only 3.9%, which may potentially increase the risk of type I error. In our analysis, we employed Cox-proportional hazards model to account for the time to event variable, instead of simply dichotomizing the outcome as alive or death (22).
One strength of the present study is that fractional polynomials model was employed to account for the potential non-linear relationship between lactate and hazard. An important shortcoming in previous studies investigating lactate and mortality lies in that the fact that none of them examined the model adequacy by testing the linear assumption of the covariates with logit function. If the linear assumption is violated, the regression model will be invalid and odds ratio obtained from the model may not be hold true across full ranges of lactate value (14-23). Therefore, we used fractional polynomials model to identify the best fit model. Our result showed PF(2) with the power of –2 and –1 had the smallest deviance. As compared with other models (model without lactate, linear, FP1), the deviance difference of FP(2) was statistically different from others. The result confirmed our hypothesis that the relationship between initial lactate and hazard was non-linear. As shown in Figure 2, the slope of the function is steep between 4 to 10 mmol/L, and after that the steepness gradually attenuates. This finding suggest that resuscitation bundle aiming to improve tissue perfusion and entailing lactate clearance can benefit the most for patients with lactate level between 4 and 10 mmol/L. For patients with very high lactate beyond 15 mmol/L, the probability of survival may be small and strenuous resuscitation may add little benefit. However, due to the observational nature of the present study, this finding is hypothesis-generating and requires further validation.
To the best of our knowledge, this was the first study investigated the association of normalization time with death hazard, and the time was incorporated into the model as a continuous variable. Previous studies that have explored the time for lactate clearance commonly predefined a certain time point at which the lactate value was rechecked and subjects were dichotomized into groups with and without lactate normalization. This time points were defined arbitrarily and varied across studies ranging from 6 to 72 hours (7,24-26). This time point was chosen probably because this is a time window in which aggressive resuscitation strategy may provide benefit. In our study, we found that: (I) lactate normalization was an indicator of better outcome as compared with those without lactate normalization; (II) among patients with lactate normalization, the longer it takes for normalization, the worse the clinical outcome would be. The second notion holds true when normalization time was less than 150 hours, and after that the regression model became unstable as reflected by a wide confidence band. However, 150-hour is long enough for both medical decision making and risk stratification in real clinical practice. Nevertheless, limitations in analyzing normalization time needs to be acknowledged. Because this was an analysis of a large clinical database that was not specifically designed for the investigation of lactate normalization time, the frequency of lactate measurement was completely determined by the treating physician. Bias could be introduced in situations when one has actually normalized lactate but failed to be measured. As a result, such patients were grouped as non-normalization. One way to address this shortcoming is to conduct a well-designed prospective study, by predefining the frequency and time points of lactate measurements.
Conclusions
In aggregate, our study confirmed previous finding that initial lactate was independent predictor of mortality in unselected ICU patients. What’s new in our study is that we used fractional polynomials to fit the Cox proportional hazard model, allowing for more flexibility in the shape of the regression line. Secondly, it is for the first time that we provided empirical evidence on association of normalization time with death hazard. Our study demonstrates that normalization time was positively associated with death hazard within 150 hours.
Acknowledgements
Disclosure: The authors declare no conflict of interest.
References
- Fall PJ, Szerlip HM. Lactic acidosis: from sour milk to septic shock. J Intensive Care Med 2005;20:255-71. [PubMed]
- Okorie ON, Dellinger P. Lactate: biomarker and potential therapeutic target. Crit Care Clin 2011;27:299-326. [PubMed]
- Vecchio S, Giampreti A, Petrolini VM, et al. Metformin accumulation: lactic acidosis and high plasmatic metformin levels in a retrospective case series of 66patients on chronic therapy. Clin Toxicol (Phila) 2014;52:129-35. [PubMed]
- Gjedsted J, Buhl M, Nielsen S, et al. Effects of adrenaline on lactate, glucose, lipid and protein metabolism in the placebo controlled bilaterally perfused human leg. Acta Physiol (Oxf) 2011;202:641-8. [PubMed]
- Fuller BM, Dellinger RP. Lactate as a hemodynamic marker in the critically ill. Curr Opin Crit Care 2012;18:267-72. [PubMed]
- Gunnerson KJ, Saul M, He S, et al. Lactate versus non-lactate metabolic acidosis: a retrospective outcome evaluation of critically ill patients. Crit Care 2006;10:R22. [PubMed]
- Abramson D, Scalea TM, Hitchcock R, et al. Lactate clearance and survival following injury. J Trauma 1993;35:584-8; discussion 588-9. [PubMed]
- Lee TR, Kang MJ, Cha WC, et al. Better lactate clearance associated with good neurologic outcome in survivors who treated with therapeutic hypothermia after out-of-hospital cardiac arrest. Crit Care 2013;17:R260. [PubMed]
- Puskarich MA, Trzeciak S, Shapiro NI, et al. Whole blood lactate kinetics in patients undergoing quantitative resuscitation for severe sepsis and septic shock. Chest 2013;143:1548-53. [PubMed]
- Liu XW, Ma T, Qu B, et al. Prognostic value of initial arterial lactate level and lactate metabolic clearance rate in patients with acute paraquat poisoning. Am J Emerg Med 2013;31:1230-5. [PubMed]
- Saeed M, Villarroel M, Reisner AT, et al. Multiparameter Intelligent Monitoring in Intensive Care II: a public-access intensive care unit database. Crit Care Med 2011;39:952-60. [PubMed]
- Scott DJ, Lee J, Silva I, et al. Accessing the public MIMIC-II intensive care relational database for clinical research. BMC Med Inform Decis Mak 2013;13:9. [PubMed]
- Bursac Z, Gauss CH, Williams DK, et al. Purposeful selection of variables in logistic regression. Source Code Biol Med 2008;3:17. [PubMed]
- Royston P, Altman DG. Regression Using Fractional Polynomials of Continuous Covariates: Parsimonious Parametric Modelling. Applied statistics 1994;43:429-67.
- Sauerbrei W, Meier-Hirmer C, Benner A, et al. Multivariable regression model building by using fractional polynomials: Description of SAS, STATA and R programs. Computational Statistics and Data Analysis 2006;50:3464-85.
- Marty P, Roquilly A, Vallée F, et al. Lactate clearance for death prediction in severe sepsis or septic shock patients during the first 24 hours inIntensive Care Unit: an observational study. Ann Intensive Care 2013;3:3. [PubMed]
- Murtuza B, Wall D, Reinhardt Z, et al. The importance of blood lactate clearance as a predictor of early mortality following the modified Norwoodprocedure. Eur J Cardiothorac Surg 2011;40:1207-14. [PubMed]
- Borthwick HA, Brunt LK, Mitchem KL, et al. Does lactate measurement performed on admission predict clinical outcome on the intensive care unit? A concisesystematic review. Ann Clin Biochem 2012;49:391-4. [PubMed]
- Maarslet L, Møller MB, Dall R, et al. Lactate levels predict mortality and need for peritoneal dialysis in children undergoing congenital heart surgery. Acta Anaesthesiol Scand 2012;56:459-64. [PubMed]
- Hajjar LA, Almeida JP, Fukushima JT, et al. High lactate levels are predictors of major complications after cardiac surgery. J Thorac Cardiovasc Surg 2013;146:455-60. [PubMed]
- Badreldin AM, Doerr F, Elsobky S, et al. Mortality prediction after cardiac surgery: blood lactate is indispensible. Thorac Cardiovasc Surg 2013;61:708-17. [PubMed]
- Altman DG, Bland JM. Time to event (survival) data. BMJ 1998;317:468-9. [PubMed]
- Schmidt CO, Ittermann T, Schulz A, et al. Linear, nonlinear or categorical: how to treat complex associations in regression analyses? Polynomialtransformations and fractional polynomials. Int J Public Health 2013;58:157-60. [PubMed]
- Husain FA, Martin MJ, Mullenix PS, et al. Serum lactate and base deficit as predictors of mortality and morbidity. Am J Surg 2003;185:485-91. [PubMed]
- McNelis J, Marini CP, Jurkiewicz A, et al. Prolonged lactate clearance is associated with increased mortality in the surgical intensive care unit. Am J Surg 2001;182:481-5. [PubMed]
- Arnold RC, Shapiro NI, Jones AE, et al. Multicenter study of early lactate clearance as a determinant of survival in patients with presumed sepsis. Shock 2009;32:35-9. [PubMed]


