Rationales for an accurate sample size evaluation

Why size matters

Clinical research is generally a matter of investigating pertinent questions regarding a condition and its management. In an ideal world, the answers to those questions are best answered by looking at every person with that condition or its risk factors. In reality, this is hardly feasible because most conditions studied can involve a very large population. To conduct any observational study in the entire population would involve prohibitive logistical and cost issues. If the study were interventional in nature, this would be almost impossible on ethical grounds given the potential risk the population would be exposed to.

A central tenet of clinical research is therefore the concept of sampling. The idea is to conduct the research on a selected subset of the population with the expectation that that subset is representative of the whole. The sample is selected from the whole population, is fewer in number, and yet adequately reflects the whole population so that reliable inferences about that population can be drawn from the results obtained in the study.

An example may be a clinical study about intervention ‘X’ for lung cancer in China. It is obviously impossible to look at every person in China who has lung cancer, and so sampling is a must. In this situation, the “population” is the complete set of people (all persons with lung cancer in China), and the “target population” is the subset of individuals with specific clinical and demographic characteristics that allow intervention ‘X’ to be performed (for example: males, between ages 40 and 60, with confirmed adenocarcinoma). The “sample” is a further subset of the target population selected for this study that is representative of the whole. This selection can be performed by a variety of methods, including both random or some pre-defined systematic selection process.

There are many factors that govern how representative the sample is of the whole or target population. These include how clearly the population and sample are defined, and the method used for sampling. However, perhaps the greatest determinant is simply the size of the sample. As said above, studying a very large cohort is not ideal for practical and logistical issues. However, studying a cohort that is too small can result in insufficient statistical power. That is, statistical analysis becomes unable to identify real differences as significant simply because there are not enough subjects to analyze. Furthermore, a sample that is too small carries the possibility that excessive selection was performed, so that the final sample may not truly be representative of the population.

The key in clinical research therefore lies in sampling a number of subjects that is neither too many nor too few. Thankfully, identifying the minimum number of subjects to yield reliable results from statistical analysis is not entirely guesswork. Statistical tools exist which can help to estimate the minimum sample size required. This brief review discusses the rationale behind basic sample size estimation for clinical research. It is aimed at the complete novice to this field (those looking for a more in-depth exploration of this subject are advised to refer to the ‘Further Reading’ list at the end).

Why should I estimate sample size?

The above explains the importance of sample size to a clinical study. On purely scientific grounds, sample size estimation is necessary to allow the study to show any significant result if it exists whilst avoiding the recruitment of an excessively large sample cohort. However, there are a couple of more practical reasons why an academically-minded physician should perform sample size estimation.

First, in order to obtain permission to perform any clinical research (especially experimental studies involving interventions), ethical approval must be obtained from the investigator’s institutional review board. Today, virtually all such boards in almost all countries would require a sample size estimation to justify the investigator’s application to recruit subjects. The board’s interest lies in ensuring that: (I) exposure to any potential risk from the intervention is limited to as few subjects as possible; and (II) the study has a reasonable chance of identifying significant results (in other words, subjects are not exposed to risk for the sake of a study that has no hope of yielding meaningful conclusions). Failure to meet either or both of these conditions would mean that it is probably unethical to proceed with the study.

Second, editors and reviewers of the major medical journals nowadays expect sample size estimation to be routinely performed in any clinical study involving statistical analyses comparing study arms. The study’s statistics especially come under scrutiny if the authors suggest no difference between the study arms. It is all too easy for the average reviewer to ask: is that failure to detect a difference simply because the sample size was too small? To some inexperienced authors, when the reviewer notes this criticism, it is often too late. Because the study had already been done, it is not really possible to then go back to perform a sample size estimation and then seek to add more subjects to accumulate an adequate cohort. By the time this criticism is made, the paper—and the study behind it—are probably no longer easily salvageable.

What the two situations above highlight is not only that sample size estimation should be done for almost any clinical study, but that it should be done early. Indeed, it needs to be done ideally during the design of the methodology itself, and certainly before subjects are recruited. This is the only way to ensure institutional review board approval of the study, and to minimize the chance that journals will reject the eventual paper submitted. Identification of any problems in sample size before the study begins in earnest also allows for changes to be made before it is too late.

Study design: hypothesis testing

When designing any clinical study, it is important to realize that the core of most such studies is the testing of a hypothesis. The investigator’s own clinical observations, reading into the literature around a topic, or inferences from previous research has led to a pertinent question about that topic for which no good answers yet exist. Stating that question in a simple and specific way—along with a proposed answer—forms the basis of a hypothesis. The clinical study is simply a means of testing that proposed answer or hypothesis. This is the scientific method.

In many major studies, the hypothesis is framed as a null hypothesis. This means that the investigator proposes that two (or more) variables have no association with or effect on each other. If the study produces results that disproves or rejects this hypothesis, it therefore means that an association did exist. An example would be to hypothesize that smoking is not related to an increase risk of lung cancer. An alternative hypothesis can also be framed, proposing that the two (or more) variables are related to each other. This can be one-sided (example: smoking increases the risk of lung cancer), or two-sided (example: smoking has an effect on the risk of lung cancer).

The role of the study itself is to collect data which can then be statistically analyzed to see if any association really does exist between the variables studied. The investigator looks to see if the evidence produced supports the null hypothesis, or whether it rejects it in favor of an alternative hypothesis.

The problem with any clinical study—even the most meticulously designed and executed—is that the data can potentially lead to wrong conclusions when analyzed statistically. These can be classified as two types of statistical error:

• Type I error (false-positive): an association between the variables is somehow identified on statistical analysis when none actually exists, so that the null hypothesis is wrongly rejected;
• Type II error (false-negative): the statistical analysis fails to detect an association between the variables when such an association actually exists, so that the null hypothesis is not rejected when it should be.

Mathematically speaking, it is impossible to entirely eliminate the possibility of such errors. The best that investigators can do is therefore to minimize the chance of such errors occurring. This is done by selecting a suitable sample size for the study. The probability of both type I and type II errors is reduced with increasing cohort size. The aim of sample size estimation is therefore to choose a sufficient number of subjects to keep the chance of these errors at an acceptably low level while at the same time avoiding making the study unnecessarily large (leading to cost, logistical and ethical problems).

The ingredients for sample size calculations

To estimate the required sample size for a study, the investigator must first identify the primary outcome measure for the study. The sample size calculations are then geared towards finding a suitable sample size to identify a significant result in this primary outcome measure. If more than one outcome measure is important to the study, sample size estimations should be conducted for each outcome measure, and then the largest sample size estimated should be the one used in the study.

For each outcome measure in each study, the sample size estimation requires that the investigator first defines a number of quantities. There are four essential ‘ingredients’ used to prepare a suitable sample size: (I) effect size; (II) variability; (III) significance level; (IV) power.

Effect size

For the outcome measure studied, the investigator needs to define what degree of difference in that measure is being looked for. For example, this could be a difference of 10% in 5-year survival rates between smokers and non-smokers, or a difference of 5 kg in weight loss between users of drug ‘X’ and a control group, or a difference of 1 extra day of in-hospital stay after surgery using two different techniques. The greater the difference being looked for, the smaller the sample size required to look for it. On the other hand, if the effect size being looked for is very small, a larger sample may be needed to look for it. Selecting a suitable effect size for the sample size estimation may require reference to previous studies on the subject. For example, if previous similar studies have suggested that a difference of around 1 day in post-operative stay is generally noted between patients receiving different surgical techniques, then it is reasonable to look for an effect size of 1 day in this current study. If no previous similar studies exist, the investigator may choose to first conduct a pilot study to gain some initial experience and data, and to use the latter to help design a more sophisticated study with sample size estimation subsequently. Ultimately, good clinical sense should help guide what effect size is being looked for. As a rule of thumb, the smallest effect size that would be clinically meaningful (and/or must not be overlooked) should be chosen. For example, if the length of stay after an operation is usually 4 days then a difference of 1 day shorter stay using a new technique may be considered meaningful, because that would mean a 25% faster discharge for patients. However, in the same situation, looking for a difference of 6 hours may not be so helpful because in practice a surgical team would not reassess whether to send a patient home every 6 hours (so finding a difference of 6 hours has no real clinical relevance). In formulae for sample size estimation, effect size is conventionally denoted by ∆.

Variability

The discussion above about effect size perhaps over-simplifies things. In reality, the difference in the outcome measure between two study arms may not be so clear-cut because considerable variation can exist in that effect within the same study arm, resulting in considerable overlap. For example, if one is looking for a difference of 5 kg in weight loss between users of drug ‘X’ and a control group, but individuals in both groups can vary between a weight loss of 25 kg to a weight gain of 20 kg, then it becomes much more difficult to demonstrate a difference between the study arms. The inherent variability within the cohort studied is best expressed as the standard deviation, usually denoted by σ.

Significance level

The level of significance is essentially the same as the chance of a type I error, and is denoted by α. It refers to a cut-off level of probability (set by the investigator) below which the null hypothesis is considered rejected. In other words, if the statistical test used finds that the probability of the study result is even lower than α, then the investigator would say that the alternative hypothesis is true. In most medical research α is usually set at 0.05—because a result that occurs despite a probability of occurring by chance of less than 5% is widely accepted to be ‘significant’. The higher the α value set by the investigator, the more likely the null hypothesis is rejected, but the more likely a type I statistical error can occur (null hypothesis falsely rejected).

Power

The chance of a type II error (null hypothesis not rejected when it should be) is denoted by β. The power of the study is 1-β. Basically, the greater the power of a study, the less likely the null hypothesis is not rejected when it should be—or the greater the chance that the statistical analysis will identify the result of the study as significant if it should be. Again, when performing a sample size estimation, the investigator is in theory free to state the power he/she desires the study to possess. In actual practice, many investigators would say that a type II error rate of 20-30% may be reasonable, and hence a power of 70-80% is commonly chosen. If a study is considered especially pivotal or large, the power may even be set at 90% to reduce the possibility of a false negative result to 10%.

In addition to the four basic ‘ingredients’ above, there are also other factors (‘seasonings’) that the investigator may factor in during the sample size calculations. These may be taken into account with some of the sample size calculation methods available (‘recipes’):

• Underlying event rate of the condition under study (prevalence rate) in the population;
• Expected dropout rate;
• Unequal ratio of allocation to the study arms;
• Specific considerations related to the objective and design of the study.

The recipes for sample size calculations

Once the above basic ingredients are acquired, many ‘recipes’ (methods) that can be used to combine these to estimate a sample size are widely available.

Each ‘recipe’ may be designed to be applicable only for:

• Two or more of the four basic ‘ingredients’, with/without one or more ‘seasonings’;
• Specific statistical test(s) that will be used to analyze the study data (most commonly a t-test or a Chi-squared test).

Investigators may choose whichever ‘recipe’ best suits the study being conducted and/or the investigator’s own experience. In many cases, it may be prudent to seek the advice of a biostatistician to help select the most appropriate sample size calculator recipe.

The sample size calculator recipes can be generally classified as follows.

General formulae

Many formulae exist into which the above ingredients can be inserted to calculate a sample size estimation. One commonly used example for studies comparing two means using a t-test is:

n, required sample size; Z_α, constant according to the significance level α; Z_1-β, constant according to power of the study; σ, standard deviation; ∆, estimated effect size.

An example of using this formula could be a randomized controlled trial investigating the use of a hemostat ‘X’ to reduce blood loss during lung surgery. In this example, a 2-sided t-test is used and the investigator defines that a significance level α of 0.05 is acceptable, and a power 1-β of 80% is desired. Using pre-defined tables, this gives values for Z_α and Z_1-β of 1.96 and 0.8416 respectively. From previous papers, the standard deviation in blood loss in such operations is 100 mL. The investigator is interested in a reduction in blood loss (effect size) of 20 mL. Put these numbers into the formula above, one gets:

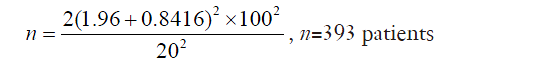
The calculator estimates that a minimum of 393 patients should be included in the trial. If the investigator expects 10% of the patients to drop out of the study for one reason or another, for example, this might constitute a ‘seasoning’ to add to the calculations, and the investigator may choose to recruit at least 432 patients.

Quick formulae

The above general formulae can often be complex. However, in many studies, the statistical tests used and the α and 1-β levels set are very standard. Therefore, for convenience, some quick formulae exist that assume standard tests and standard ‘ingredients’ to be used, and hence allow much simpler-to-use calculations.

A good example is Lehr’s formula. This recipe can be used if the statistical analysis used is a t-test or Chi-squared test, and it assumes the α and 1-β values are set at 0.05% and 80% respectively. With these assumptions, the formula:

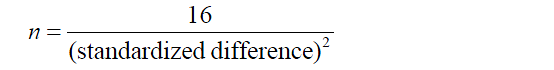
If an unpaired t-test is used, the standardized difference is ∆/σ. It is obvious that this quick formula is much easier to remember and use than a general formula, although one must pay attention to the conditions and assumptions for its use.

Nomograms

These are specially designed diagrams on which values of the basic ‘ingredients’ can be used to indicate the required sample size. The classic example is the Altman’s nomogram which can be used for paired or unpaired t-tests, as well as for Chi-squared tests. It consists of two vertical axes at the left and right of the nomogram, with a diagonal axis in-between. The left vertical axis has values for the standardized difference (which can be calculated from the basic ingredients depending on which test is used), the right axis has values for the power (1-β), and the diagonal axis has values for sample size. A straight line can be drawn joining the values for standardized difference and power on the left and right axis, and where this line intersects the diagonal axis will indicate the required sample size.

Special tables

Tables have been drawn up by statisticians to easily show the sample size required for particular tests (e.g., t-test and Chi-squared test). Definition of the ‘ingredients’ allows the correct table to be referenced to yield the sample size required.

Computer software

Although very useful, the nomograms and tables above have been largely replaced by the even more convenient computer software-based recipes. These programs are readily available online and also in the form of apps for mobile devices. Investigators not only have handy access to sample size calculations at any time, but they no longer need to worry about memorizing formulae and calculations. Simply inputting their desired values for the ingredients is sufficient. The convenience also means that investigators can easily experiment with changing the ingredient values to instantly see what effect these may have on the required sample size. Furthermore, many such calculators allow results to be displayed in graphs or tables. The biggest downside to such convenient access is that investigators may find it difficult to choose between the many calculators on offer. It is perhaps fair to say that many investigators may not be able to easily distinguish which calculator is most suitable for his/her study.

Serving up the sample size estimate

Once the ingredients and seasonings have been prepared using an appropriate recipe, the final product—the sample size estimate—needs to be served. There is a generic way to do this: a ‘power statement’ should be written. This is to be included in the study proposal to the institutional review board, and also in the final research paper for the study. A typical power statement may read: “Sample size calculation determined that to have a (1-b) chance of detecting a difference of D at the level of significance using (statistical test), n patients were required”.

The example above about the use of hemostat ‘X’ can again be used. In this scenario, the power statement would perhaps read: “Sample size calculation determined that to have a 80% chance of detecting a difference of 20 mL of blood loss at the 5% level of significance using 2-sided t-test, 393 patients were required to be included in this study”.

Conclusions

The analogy between sample size estimation and cooking is quite apt. The calculation is only possible if the basic ingredients are first defined and collated (effect size, variability, significance, power). Seasoning considerations may help flavor the calculation to better suit the study’s needs. The investigator then has a plethora of different recipes to choose from in order to prepare the final sample size estimation. The final product—like good food—provides nourishment for the whole clinical study. Without such sustenance, the study may be too weak to pass the harsh scrutiny of the institutional review board or journal editors. In order to nourish the study, the sample size estimation must be prepared and consumed early, before the study starts in earnest.

It is hoped that this brief article will provide the reader with enough food for thought regarding the rationale for sample size calculations in clinical research!

Further reading

• Altman DG. How large a sample? In: Gore SM, Altman DG, editors. Statistics in practice. London: British Medical Association, 1982:6-8.
• Hulley SB, Cummings SR, Browner WS, et al, editors. Designing Clinical Research, 4th Ed. Philadelphia, USA: Lippincott Williams & Wilkins, 2013.
• Inouye SK, Fiellin DA. An evidence-based guide to writing grant proposals for clinical research. Ann Intern Med 2005;142:274-82. [PubMed]
• Kirby A, Gebski V, Keech AC. Determining the sample size in a clinical trial. Med J Aust 2002;177:256-7. [PubMed]
• Larsen S, Osnes M, Eidsaunet W, et al. Factors influencing the sample size, exemplified by studies on gastroduodenal tolerability of drugs. Scand J Gastroenterol 1985;20:395-400. [PubMed]
• Lehr R. Sixteen S-squared over D-squared: a relation for crude sample size estimates. Stat Med 1992;11:1099-102. [PubMed]
• Machin D, Campbell MJ, editors. Statistical Tables for the design of clinical trials, 2nd Ed. Oxford: Blackwell Scientific Publications, 1995.
• Petrie A, Sabin C, editors. Medical statistics at a glance. Oxford: Blackwell Scientific Publications, 2000.

Acknowledgements

None.

Footnote

Conflicts of Interest: The author has no conflicts of interest to declare.