The game theory in thoracic surgery: from the intuitions of Luca Pacioli to the operating rooms management
Introduction
Game theory is a formal way to analyze the interactions among groups of subjects who behave each other. Otherwise, the game is a simple series of independent decisions problems and the players account for this interdependence choosing their best action (1). It has historically been of great interest in the economic fields in which decisions are made in a competitive environment; however, it has been applied to various disciplines ranging from philosophy to biology, from business to medicine (2).
A brief history of game theory
Game theory has attracted in the history greatest mathematicians. The first report of game theory was in Talmud (early years of the first millennium) about the division of an inheritance. In the Distinctio Nona-Tractus Decimus of his Summa, the medieval priest Luca Pacioli describes (Figure 1), amongst other peculiar logical problems (so called De Straordinariis), the quandary n. 50, also known as the ball problem (or Balla, from ancient Italian). The quest proposed by Pacioli, which has been variously addressed in different times thereafter (score problem as well as problem of the parts), has been recognized, in the history of mathematics, as a fundamental step in the development of the modern probability calculation (3). Besides the obscurity of Pacioli’s writings and the scarce knowledge we have nowadays about the ancient game, he has taken as example in describing this dilemma, the formulation of the problem still remains quite plan. We should suppose that two player of equal skills played a string of sessions (or turns) in a given game, no matter what, given the agreement that the one who would score a predetermined number of points would win the match. For whatever reason, the match is cut short before the aforementioned score is reached. Given this premature end, how should the prize be divided in parts and distributed between the contesters? The problem is proposed by the priest in the following terms: the player of a ball-based game wins when he reaches 60 points, the game consisting in flinging a ball towards the competitor with the aim of hitting him (some sort of dodge ball). Every successful blow brings 10 points (ending the turn). After this premise, the match is stopped after seven turns, so that one player (named A) has reached 50 points (5 blows on target), while the other one (named B) only 20. The winner had been previously promised 10 golden coins (the prize or jackpot). How should the 10 coins be distributed between the two players? From the XIV century henceforth, various solutions have been proposed, some of them being described in mathematics essays concerning abacus calculation ever since the 1400s (4). Pacioli’s work lists several of those previous solutions, referred as opinions about the problem. Despite those opinions, he argues that the fairest solution might be achieved in three ways:
- We should take into account the maximum number of turns that might be played. In the given circumstances, there is a maximum of 11 turns. If one player wins with 60 points, and every turn accounts for 10 points, the longest possible game should finish with the following score: 60 to 50, therefore needing 11 turns. If P is the prize (10 golden coins), a and b are the stakes won respectively by the player A
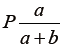 , and B
, and B 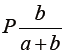 the prize should be handed out as follows: 5/7 to A (about 7.14 coins) and 2/7 to B (2.86 coins).
the prize should be handed out as follows: 5/7 to A (about 7.14 coins) and 2/7 to B (2.86 coins). - The second way is pretty similar, although it considers the maximum amount of points instead of turns (110 points). At the end the proportion remains the same, 5/7 and 2/7.
- The third approach is based on a simple proportion. The sum of the points of the two contenders is 50+20=70, which corresponds to the whole bet (again, 10 golden coins). Therefore, the player who scored 50 points should receive x coins, calculated as follows:
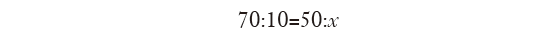
whereas the other player should receive y, which is
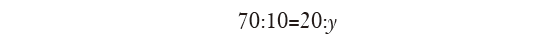
The solution stated by Pacioli had been widely criticized, first of all by Gerolamo Cardano and then by Niccolò Tartaglia. The two scientists argued that the problem of parts should not be solved by proportions, such as the problems concerning the distribution of bonuses between two partners in a mercantile venture. Following that route would certainly bring about paradoxical results. In particular Tartaglia, in his General Trattato, speculates that, given the same rule (the game is won when one player scores 60 points), the match stopped abruptly after one player has scored 10 points, while the other player 0. We should reckon that, at this given point, both players would have good changes to win the game, since there are still plenty of points to dispute. Under those particular circumstances, the Pacioli’s solution is deemed very unfair by Tartaglia, owing the fact that the rule of proportion would assign the whole prize to the player who scored just 10 points (5). In order to cope with the inherent iniquity of Pacioli’s solution, Tartaglia postulates a less mischievous system, trying to balance those possible unfair results. For instance, if the player A scored a and player b scored b, with a>b, A should receive half the value of the jackpot (which is 5 golden coins in our example), plus the proportion 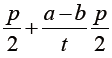 . Anyway, also in the case proposed by Tartaglia, the risk of iniquity is rather high, owing the fact that, in the peculiar situation of a game stopping when the player A is about to win, and B has practically no changes, the Tartaglia’s solution would excessively benefit the supposed loser. Despite that, Tartaglia would have played his role in the final solution of the balla problem.
. Anyway, also in the case proposed by Tartaglia, the risk of iniquity is rather high, owing the fact that, in the peculiar situation of a game stopping when the player A is about to win, and B has practically no changes, the Tartaglia’s solution would excessively benefit the supposed loser. Despite that, Tartaglia would have played his role in the final solution of the balla problem.
Blaise Pascal, in a letter to Pierre de Fermat dating 29th July 1654, calculates the players’ possibility to succeed when the game prematurely stops by means of the combinatory calculation which employs the arithmetical triangle, also known as Pascal’s Triangle, but which had already been described by Tartaglia, in the second part of his Trattato. The correspondence between Pascal and Fermat should be considered as the first step of the Probability Theory. In those six letters, we may find the linchpin of the combinatory calculation, whilst some interesting properties of numbers are unraveled (6). By applying the method of complete induction, Pascal came up with the following conclusion about combinations
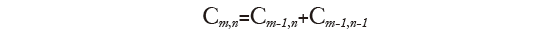
and then employed this formula in order to build up his triangle. From the systematic study of the triangle, the discovery of other properties of combination ensued, as well as the solution for the problem of the parts (7). In its simplest enunciation, Pascal figures that the two players invested 32 coins each on a particular game (so that the jackpot will be 64 coins). The player who wins three games wins also the match (and the prize as well). Therefore, if the player A wins three games he will gain the whole jackpot. Let’s consider the particular case of an abrupt stop occurring after the player A has won 2 games and the other, called B, only one. If the match continued and A would either win the following game, or lose it, thereby winning the whole jackpot (64 coins) in the first case and 32 in the other case. If the two parts decide to give up playing, A should receive 32 coins, which he would certainly be obtaining, even after losing the hypothetic fourth game, plus half the quote invested by B (16 coins), totaling 48 coins (8). The method proposed by Pascal, besides lacking the magnitude of a general theory of probability, acquires a peculiar importance within the landscape of the game theory, since, besides the problem of knowledge, it deals also with the decision process (9).
The formal study of game theory started in 1944 with the studies of John von Neumann and Oskar Morgenstern. During the World War II, the American military, for the first time in its history, recruited scientists, mathematicians, and economists and used them to help win the war. In these years, game theory research was of great interest for the Royal Air Force and the British Royal Navy to improve the hit rate in the campaign against German submarines (10). After the war, the researches in game theory focused on finding sets of strategies, known as equilibrium, to solve a game if all players behaved rationally. The most famous of these equilibria is the Nash equilibrium, proposed by John Nash (recently died and made famous in the 2001 Ron Howard’s film A Beautiful Mind). The axiom of Nash’s research is that each player acts independently (without collaboration or communication with any others) and this principle appears evident in the famous game theory scenario of the prisoner’s dilemma. After a mugging, two robbers are captured and imprisoned by the police; each captive have the choice to betray his partner in crime. With two strategies (talk and betray or be silent) available to both players, four combinations are possible. A 2×2 payoff matrix for each captive can be constructed (Table 1). This is an instance of a symmetric game, where the payoff matrix for prisoner A is the transpose of that for prisoner B. Neither captive can communicate with his partner due to the non-collaboration states. The Nash equilibrium of this game assigns a strategy to each player that will maximize the payoffs thorough a two criteria solution: the self-interest (or the desire of maximize the payoffs), and the rationality (all players are self-interested) (1). In other more complex games, we can have cooperation between players. In the cooperative games, the players can jointly increase their income and decide how the income is distributed among them. The solution for the equilibrium in a cooperative game satisfies a Pareto-optimal condition (a better solution for one player and not worse for the other player does not exist), is symmetric (in same condition, two players must have same income) and is independent to alternatives (2).

Full table
This paradigm is often used in population dynamics, where an individual’s survival and reproductive success depend on the phenotypic interactions with its competitors. Most classical game theory predict that players will reach outcomes from which no player can increase the own payoff unilaterally (11).
Example of applications of the game theory in medicine
Game theory has fascinating potential, if applied in the medical science. In oncology, as there can be many possible equilibrium states for cancer cells, there is always at least one equilibrium state. Involving the steady state population dynamics and maximizing the fitness, the evolutionary stable strategy is a strategy with a symmetric equilibrium state, or, in other words, a more stable strategy. The fitness is the average number of extra offspring that carry a specific trait into the next generation. Each player maximizes its fitness not by rational analysis of its competitors, but rather thorough dynamic convergence to a stable outcome (1). The competition, such as between the cooperator and cheater cells in a tumor, is a zero sum game, where a conflict of interests between two players produce a winner and a loser. Natural selection prefers competitors who enhance their fitness at the expense of other competitors’ fitness. While circumstances appear to create a win/lose competition among individuals, this narrow view of selection undermines the evolutionary utility of cooperation, even among competing individuals (1). The evolution game theory has been used to model the progression of cancer (12). The interaction of elements can change by genetic mutations or by changes in the biological networks. The evolutionary game theory in cancer has been proposed to model the cooperation among a heterogeneous population in sharing resources (13). In addition to the traditional view of the origin of cancer, the cooperation in cancer can also play various roles in cancer progression (14). The mathematical models inspired by evolutionary game theory are useful in clinical practice in the trial design and in the outcome prediction (15). In cancer dynamics, game theory can theoretically be used to understand the process of cancer growth. Reducing the fitness of malignant cells compared with the fitness of normal cells, cancer cells could be potentially eradicated by natural selection (16). Nevertheless, these theories have some problems when applied to clinical oncology. The reasons why a cancer cell is a game player that can make rational choices are unclear; this lack of rational behavior is a fundamental limit to the application of game theory (16). Immortalized cells develop and do not interact rationally with normal cells to maximize the combined payoffs. The behavior of cancer cell is not similar to the physiologic evolutionary behavior; therefore, they pass on mutated genes to mostly clonal offspring, until all the desired resources are consumed and, consequently, they die along with the host.
In clinical practice, the interaction between a surgeon and a patient can be described using game theory (17). A patient with a history of previous first episode of pneumothorax has breathless and chest pain and goes to the Emergency Department requiring a chest roentgenogram. At the physical examination, the breathe sounds are bilaterally present and the peripheral saturation of oxygen is normal. If he has a pneumothorax, the rational choice for the doctor is to perform a chest X-ray and to treat him. However, if he has not a pneumothorax, the execution of repetitive chest radiographs is not correct but it is still in the doctor’s best interest to treat the patient. Otherwise, the patient will give him a low satisfaction. A hypothesis of game theory is that the surgeon will prescribe radiography to all patients. This clinical situation could be explained with a prisoner’s dilemma when both captives play their best strategy and together they are worse off. Fundamentally, when different values are involved, there is an inevitable trade-offs in the consequences experienced by different players. However, regardless of the initial values of the utilities, a sizeable proportion of the simulations resulted in an inappropriate under or overtreatment. Obviously, the precise answer remains an open empirical question. In general, has been described some generic findings (18). When the patient’s utilities clearly indicate that the dominant strategy for the patient is to trust the surgeon, the surgeon should choose whatever he thinks is best for the patient. When the surgeon’s utilities clearly indicate that the dominant strategy is to recommend the treatment, the patient’s best strategy is to choose to trust the surgeon (expected benefits outweigh the expected harms for the given probability of disease). When the surgeon’s utilities indicate that the strategy of recommending against treatment is dominant, the patient should trust the surgeon regardless of his own utilities. When neither strategy is dominant, a rational approach would be to randomize the strategy of choice. When the probability of a clinical event is high, the best strategy for the surgeon is to recommend treatment and for the patient to trust the surgeon and accept his recommendation.
Another example of application of game theory is management of the operatory theater program. Many poorly run operating rooms have adopted a culture of mutual defection and self-centered behavior. In an effort to minimize the irrational nature of operating room management, daily operational decisions should follow the rationally ordered priorities: maintain the patient safety, open the access to the operatory room, maximize the operatory room efficiency, reduce the patient waiting times, and increase the personal satisfaction (19).
Conclusions
Game theory focuses on how groups of people interact themselves. Few papers have been written about the application of game theory in surgery. The majority of scenarios of game theory in surgery fall into two main groups: cooperative and no cooperative games. No cooperative game theory (how intelligent individuals interact with one another in an effort to achieve their own goals) is the most applicable in surgery. Nevertheless, multiple interactions (as cooperation) in the operating room settings can create a better synergy and can improve the efficiency of the hospital and the safety of patients.
Acknowledgements
None.
Footnote
Conflicts of Interest: The authors have no conflicts of interest to declare.
References
- Cleveland C, Liao D, Austin R. Physics of cancer propagation: A game theory perspective. AIP Adv 2012;2:11202. [PubMed]
- Delorenzo C, Papademetris X, Staib LH, et al. Image-guided intraoperative cortical deformation recovery using game theory: application to neocortical epilepsy surgery. IEEE Trans Med Imaging 2010;29:322-38. [PubMed]
- Barra M. Il “problema della divisione della posta in gioco” e delle valutazioni di probabilità: 500 anni di storia – Soluzione bayesiana. In: Frosali G, Ottaviani M, Editors. Il pensiero matematico nella ricerca storica italiana. Ancona: Tipolitografia Trifogli, 1993:143-74.
- Toti Rigatelli L. Il problema delle parti in manoscritti del XIV e XV secolo. In: Folkerts M, Lindgren U, Editors. Mathemata. Stuttgart: Steiner Verlag, 1985:229-36.
- Tartaglia N. General Trattato di numeri e misure. Venezia: Curtio Troiano dei Navò, 1556:c. 265v. Available online: http://www.e-rara.ch/doi/10.3931/e-rara-19205
- de Fermat P. Œuvres (cured by Tannery P, Henry C). Paris, 1894:288-314. Available online: http://www.encyclopedia.com/topic/Blaise_Pascal.aspx
- Keith D, editor. La lettera di Pascal. Storia dell’equazione che ha fondato la teoria della probabilità. Milano: Rizzoli, 2008.
- de Fermat P. Œuvres (cured by Tannery P, Henry C). Paris, 1894:290. Available online: http://www.encyclopedia.com/topic/Blaise_Pascal.aspx
- Altini C. Human nature in the contemporary world. Arch Int Hist Sci (Paris) 2014;64:245-6. [PubMed]
- Capps D. John Nash, game theory, and the schizophrenic brain. J Relig Health 2011;50:145-62. [PubMed]
- Sanfey AG. Social decision-making: insights from game theory and neuroscience. Science 2007;318:598-602. [PubMed]
- Deisboeck TS, Zhang L, Yoon J, et al. In silico cancer modeling: is it ready for prime time? Nat Clin Pract Oncol 2009;6:34-42. [PubMed]
- Axelrod R, Axelrod DE, Pienta KJ. Evolution of cooperation among tumor cells. Proc Natl Acad Sci U S A 2006;103:13474-9. [PubMed]
- Hanahan D, Weinberg RA. Hallmarks of cancer: the next generation. Cell 2011;144:646-74. [PubMed]
- Wu A, Liao D, Austin R. Evolutionary game theory in cancer: first steps in prediction of metastatic cancer progression? Future Oncol 2015;11:881-3. [PubMed]
- McEvoy JW. Evolutionary game theory: lessons and limitations, a cancer perspective. Br J Cancer 2009;101:2060-1. [PubMed]
- Djulbegovic B, Hozo I. When is it rational to participate in a clinical trial? A game theory approach incorporating trust, regret and guilt. BMC Med Res Methodol 2012;12:85. [PubMed]
- Djulbegovic B, Hozo I, Ioannidis JP. Modern health care as a game theory problem. Eur J Clin Invest 2015;45:1-12. [PubMed]
- McFadden DW, Tsai M, Kadry B, et al. Game theory: applications for surgeons and the operating room environment. Surgery 2012;152:915-22. [PubMed]


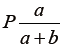 , and B
, and B 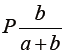 the prize should be handed out as follows: 5/7 to A (about 7.14 coins) and 2/7 to B (2.86 coins).
the prize should be handed out as follows: 5/7 to A (about 7.14 coins) and 2/7 to B (2.86 coins).
