
Uncertainty analysis of chest X-ray lung height measurements and size matching for lung transplantation
Introduction
Lung size is one of the main criteria used to determine a suitable donor-recipient match in lung transplantation (1). At a population level, under and over-sized lung allografts are associated with higher rates of surgical complications, primary graft dysfunction, one year mortality and shorter time to developing chronic lung allograft dysfunction (2-7). At the individual level, it is difficult to predict size mismatch. Despite these findings there is no consensus on the best method for size matching in lung transplantation. Transplant centers use a variety of methods to size match donors and recipients independently or in combination (Table 1). The most common tools are predictive equations and radiographic estimates of lung size. Practice patterns indicate that “real” lung size matters with systematic acceptance of larger donor lungs for recipients with chronic obstructive pulmonary disease and cystic fibrosis and smaller donor lungs for recipients with interstitial lung disease (8).
Table 1
| Size matching method | Advantages | Limitations |
|---|---|---|
| Predicted total lung capacity | • Unbiassed by underlying disease process • Easy to calculate • Applicable to donor and recipient • Outcome data available |
• Wide confidence interval of the predictions • Precision of the estimates can only be improved marginally • Does not consider the underlying disease process |
| Pulmonary function tests (TLC, FVC) | • Accurate estimate of lung volumes | • Only available for recipient in clinical practice • Biased by underlying lung disease |
| Inframammary chest circumference | • Simple • Attempts to measure actual lung volume • Available for donor and recipient |
• Inaccurate estimates of lung volume • Affected by obesity • Error in measurement |
| Chest X-ray (Linear, planimetric measures) | • Simple • Accurate estimates of TLC under study conditions • Available for donor and recipient • Outcome data available |
• Precision and accuracy unknown in clinical setting • Biased by underlying disease |
| Computed tomography volumetry | • Accurate estimates of TLC under study conditions • Provides additional anatomical information related to donor quality |
• Limited clinical data • Precision and accuracy unknown in clinical setting • Not routinely available |
TLC, total lung capacity, FVC, forced vital capacity.
The use of predictive total lung capacity (TLC) equations has the theoretical advantage of providing TLC estimates unbiased by the underlying disease of the recipient or the use of mechanical ventilation in the donor. Predicted TLC equations are meant to differentiate healthy and diseased individuals and were not designed to be precise at the individual level (9). For this reason, they have wide confidence intervals. As an example, an average healthy male in the United States is 179 cm tall, and his predicted TLC ranges between 5.3 and 7.7 liters (10-12). This lack of precision is a barrier to establishing the acceptable limits of size discrepancy.
Chest X-ray (CXR) linear measurements are the most common method used to estimate the “real” TLC during donor-recipient matching. We refer to linear measurements as lung heights. Lung heights strongly correlate with TLC (13,14) and they are also subject to uncertainty (15). This uncertainty has not been previously described in clinical transplantation. Uncertainty can be secondary to systematic and random errors in measurement and can be described by agreement and error analysis (15,16). Furthermore, for size matching, measurement errors in both the donor and the recipient must be accounted for. Error propagation theory can be used to describe the final uncertainty after subtracting donor and recipient lung heights.
We hypothesize that CXR lung height measurements are imprecise for the purpose of size matching in lung transplantation. We will use agreement analysis and error propagation theory (15) to evaluate CXR lung height measures and the effects of measurement error and propagation on potential adjudication of donor lungs. Our goal is to improve the precision of CXR lung height by first understanding the sources of measurement error and then mitigating them. The following article adheres to the STROBE and GRRAS reporting checklists (available at https://jtd.amegroups.com/article/view/10.21037/jtd-21-1755/rc) (17,18).
Methods
The study was performed at Washington University School of Medicine - Barnes Jewish Hospital and the local organ procurement organization Mid-America Transplant (MAT), St. Louis, Missouri (US) using a retrospective cohort design. The study was conducted in accordance with the Declaration of Helsinki (as revised in 2013). The Washington University School of Medicine Institutional Review Board reviewed the protocol and waived the need for informed consent (IRB No. 202012069).
The main outcome of this descriptive study is to report the bias and limits of agreement for CXR lung heights and the final error in calculated donor-recipient lung height difference (19).
Eligible donors and recipients were numbered and then selected according to a random number generator. Twenty-five recipients listed for transplantation from 1/1/2019 to 12/1/2020 at Washington University School of Medicine - Barnes Jewish Hospital, and 25 donors from all prospective brain-dead donors managed at MAT’s independent organ recovery center over the same period were included. Donors and recipients were independent of each other. Up to 6 CXRs were measured per subject and individuals with only one CXR were excluded.
Measurements
Recipients undergo posteroanterior CXR using standard technique with the patient upright during full inspiration and 1.83 m target-to-film distance at every pre-transplant clinic visit. These visits occur at least every three months and more frequently as clinically indicated. Only CXRs obtained during the 6 months prior to transplantation were included. Donor CXRs are portable supine anteroposterior images while receiving mechanical ventilation with tidal volumes of 6–8 mL/kg and with a positive end-expiratory pressure of 10 cm H2O. Donors undergo CXR imaging as clinically indicated. The images for donors and recipients were digitally stored.
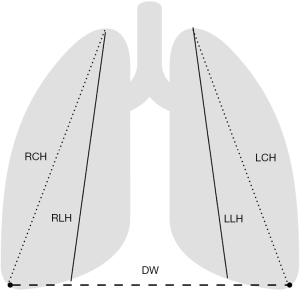
The right and left lung heights (RLH, LLH) measured from the lung apices to the ipsilateral dome of the diaphragm, the height from the right and the left apex to the ipsilateral costophrenic angle (RCH and LCH) and the diaphragmatic width (DW, the distance between the right and left costophrenic angles) were measured twice by two independent raters blinded to each other and to their previous measurements (Figure 1). The two raters were lung transplant clinicians regularly involved in the matching of donors and recipients. When the dome of the diaphragm was not apparent, the lung height was measured to the middle of the ipsilateral diaphragm. In cases were basilar infiltrates obscured the diaphragm or costophrenic angles, the raters used their best judgement to provide measurements. The measurements were performed using IConnect Access 6.2® (Merge Healthcare, 900 Walnut Ridge Drive Hartland, WI 53029 USA). Age, gender, race, and height in centimeters for both donors and recipients and the underlying diagnosis for recipients were recorded. All analyses were conducted using STATA/SE 15.1 (StataCorp, TX, USA).
Statistical analysis
Categorical data are presented as percentages and continuous data as means with standard deviations (SD).
Agreement analysis
We performed a univariate linear regression with the individual difference in lung heights as the outcome of interest and donor vs. recipient status and demographics as predictors. This preliminary step was used to decide whether data from donors and recipients could be pooled together for the analyses.
We relied on diagnostic plots for normality and Spearman correlations between individual standard deviations and individual average height to test the Bland Altman assumptions of normality in the distribution of errors and stability of the error magnitude across the range of measurements (16).
Finally, we described the agreement of repeated CXR measures by comparing the two blinded raters using ANOVA methods as described by Bland and Altman (16) and accounting for the presence of multiple measurements per individual (Appendix 1). Measures of systematic error or bias and precision including within and between subject variability and the final SD of the differences in lung heights with their confidence intervals are provided.
Error propagation
Both bias (systematic error) and precision (random error) of donor/recipient lung height measurements must be considered to calculate the final bias and precision of their difference in height. According to the error propagation theory, the final bias will equal 0 if the rater is the same and will double if the donor and recipient have different raters (15). Errors in precision are random and normally distributed, and the resulting precision error of differences in height between donor and recipient follows a normal distribution with SD = square root of (variance of the donor lung heights + variance of the recipient lung heights) (15).
Probabilities of matching according to “true lung height” differences
Since random errors in measurement are normally distributed, the best estimate of the true value is its mean (15). Therefore, we define the “true lung height” as the average of the measured lung heights for an individual. We obtain the probabilities of size-matching a donor and a recipient according to the “true lung height” difference (Donor true lung height - Recipient true lung height) using the SD of the CXR lung height difference between donors and recipients, calculated according to section Error propagation, and Z scores for Difference ± 2 Bias ± (maximum allowed height difference in cm).
Sample size
For alpha =0.05 and beta =0.2, at least 300 measurements are needed per reader to achieve a confidence interval of 0.2× standard error of the limits of agreement confidence interval (20).
Results
A total of 25 donors and 25 recipients with a median of 4 (interquartile range, 3–6) CXRs per individual and a total of 387 CXRs were evaluated twice by the 2 independent raters (Figure S1). One recipient had bibasilar radiographic infiltrates obscuring both diaphragms in each of the 6 chest X-rays resulting in differences in height greater than 3 times the SD and was excluded from the analyses. For the rest of the cohort, 29 (7.5%) CXRs had basilar infiltrates/effusions. All other variables were available for both the recipients and the donors. The average age was 47.8±2.5 years, 29 (59.2%) subjects were male and 45 (91.8%) were white. The main indication for transplantation was interstitial lung disease followed by chronic obstructive lung disease. Donors were significantly younger than recipients. All recipients were white and 4 (16%) donors were African American. Sex, height, and average CXR lung heights were similar between the study groups (Table 2).
Table 2
| Demographics and chest X-ray measurements | Donor, n=25 | Recipient, n=24 |
|---|---|---|
| Age in years, median [IQR] | 33 [25–47] | 63.5 [59–66] |
| Gender, male | 16 (64%) | 13 (54.2%) |
| Race, white | 21 (84%) | 24 (100%) |
| Height, cm* | 168.7 (±7.2) | 170.6 (±2.1) |
| Underlying diagnosis | ||
| Interstitial lung disease | 14 (56%) | |
| Chronic obstructive pulmonary disease | 8 (32%) | |
| Cystic fibrosis | 2 (8%) | |
| Pulmonary hypertension | 1 (4%) | |
| Right apex to dome of diaphragm* | 20.8 (±3.8) | 20.8 (±4.7) |
| Left apex to dome of diaphragm* | 22.6 (±3.4) | 22.8 (±4.2) |
| Right apex to costophrenic angle* | 26.2 (±4.4) | 25.2 (±5.3) |
| Left apex to costophrenic angle* | 27.6 (±4.1) | 26.8 (±4.8) |
| Costophrenic angle to costophrenic angle* | 29.5 (±2.1) | 28.7 (±2.7) |
*, units are centimeters, (± standard deviation). IQR, interquartile range.
There was no significant relationship between age, sex, donor vs. recipient, diagnostic group, race/ethnicity and the outcome of standard deviation of lung heights in the preliminary univariate linear regression. Thus, we pooled lung height measures from all the subjects to calculate the limits of agreement (LoA).
Agreement and error analysis
DW had the best agreement without bias between raters and 95% of the measurements for a given individual fell within an error range of 4.4 cm (95% CI: 4.1–4.9 cm). The RLH and LLH followed with a bias of 0.27 and 0.22 cm and an error range of 6.2 cm (95% CI: 5.9–6.5 cm) and 6.4 cm (95% CI: 6–6.8 cm) respectively. RCH and LCH had the worst agreement with biases of 0.27 and 0.3 cm and error range of 8 cm (95% CI: 7.5–8.5 cm) and 7.6 cm (95% CI: 7.2–8 cm). The main contributor to the error in lung height measurement from a random CXR was the within subject variability. Averaging individual measurements resulted in narrower LoA without substantially improving bias (Tables 3,4, Figure 2 and Figures S2-S5).
Table 3
| Parameter | Right apex to dome of the diaphragm | Left apex to dome of the diaphragm | Right apex to right costophrenic angle | Left apex to left costophrenic angle | Diaphragm width |
|---|---|---|---|---|---|
| Bias (SE) | −0.27 (±0.03) | −0.22 (±0.06) | −0.27 (±0.07) | −0.3 (±0.04) | 0.07 (±0.08) |
| Upper LoA (95% CI) | 2.8 (2.7, 3.0) | 3 (2.8, 3.2) | 3.7 (3.5, 4) | 3.5 (3.3, 3.7) | 2.3 (2.1, 2.5) |
| Lower LoA (95% CI) | −3.4 (−3.5, −3.2) | −3.4 (−3.6, −3.2) | −4.3 (−4.5, −4) | −4.1 (−4.3, −3.9) | −2.1 (−2.4, −2) |
| σ of the differences (95% CI) | 1.58 (1.48, 1.63) | 1.62 (1.5, 1.65) | 2.04 (1.75, 2.13) | 1.93 (1.8, 2) | 1.15 (1.03, 1.23) |
| Within subject variance (SE) | 2.76 (±0.06) | 2.78 (±0.2) | 4.56 (±0.1) | 4.09 (±0.14) | 1.2 (±0.04) |
| Between Subject variance (SE) | −0.26 (±0.03) | −0.16 (±0.06) | −0.4 (±0.05) | −0.37 (±0.06) | 0.12 (±0.04) |
SE, standard error; LoA, limits of agreement; CI, confidence interval.
Table 4
| Parameter | Right apex to dome of the diaphragm, mean | Left apex to dome of the diaphragm, mean | Right apex to right costophrenic angle, mean | Left apex to left costophrenic angle, mean | Diaphragm width, mean |
|---|---|---|---|---|---|
| Bias (SE) | −0.25 (±0.06) | −0.21 (±0.07) | −0.22 (±0.08) | −0.22 (±0.07) | −0.11 (±0.07) |
| Upper LoA (95% CI) | 0.52 (0.75,0.36) | 0.78 (0.58, 1.09) | 0.82 (0.60, 1.13) | 0.76 (0.55, 1.05) | 0.85 (0.65, 1.14) |
| Lower LoA (95% CI) | −1.03 (−0.87, −1.03) | −1.21 (−1.51, −1.01) | −1.26 (−1.57, −1.04) | −1.20 (−1.44, −0.96) | −1.08 (−1.32, −0.88) |
| σ of the differences | 0.39 (0.31, 0.45) | 0.51 (0.4, 0.65) | 0.53 (0.41, 0.68) | 0.5 (0.38, 0.62) | 0.49 (0.38, 0.62) |
LoA, limits of agreement; SE, standard error; CI, confidence interval.
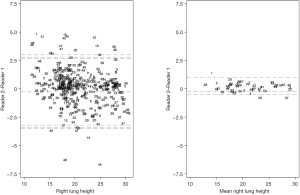
The Bland-Altman assumptions of normality in the distribution of errors and stability of the magnitude of the error across the range of measurements were met (Supplemental Results and Figures S6-S10).
Error propagation analysis
The error of the difference between the lung height of the donor and the lung height of the recipient in the case of one rater has the following standard deviations for RLH, LLH, RCH, LCH and DW respectively: 2.2 cm (95% CI: 2.1–2.3 cm), 2.3 cm (95% CI: 2.1–2.3 cm), 2.9 cm (95% CI: 2.4–3.1 cm), 2.7 cm (95% CI: 2.5–2.8 cm) and 1.62 (95% CI: 1.5–1.8 cm). Using the average lung height improves the error SDs to 0.6 cm (95% CI: 0.4–0.6), 0.7 cm (95% CI: 0.6–0.9), 0.8 cm (95% CI: 0.6–1), 0.7 cm (95% CI: 0.5–0.9), and 0.7 cm (95% CI: 0.5–0.9) (Figure 3, Figure S11, Tables S1-S8).
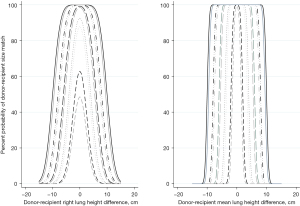
Using RLH as an example, a donor and a recipient with equal true lung heights could be considered incompatible due to random error across differences in RLH of ±6.6 cm (95% CI: ±6.3, ±6.9 cm). If the average of available CXRs is used, the donor and recipient could be considered size-incompatible across a range of ±1.7 cm (95% CI: ±1.3, ±1.9 cm) in true lung height differences. When two different readers measure the CXRs, this range is expanded by 2*bias. In the case of the RLH it would increase to ±7.1 cm (95% CI: ±6.9, ±7.4 cm) for random CXRs and ±2.2 cm (95% CI: ±1.8, ±2.5 cm) for the average RLH (Figure 3).
Figure 3, Figure S10 and Tables S1-S8 expand on the probabilities that a donor and recipient will be sized-matched according to the maximal acceptable lung height difference, true lung height difference and one or two raters.
The height from any point of the curve and its distance to the 100% mark are the probability that a given donor-recipient pair with that true lung height difference will be matched or not according to the maximal accepted lung height difference represented by that curve. The width of the base of the curve equals the range of possible size matches under different conditions (Figure 3, Figure S2). For example, if we allow a maximum RLH difference of 5 cm between the donor and recipient CXRs, the range of possible true lung height matches becomes 12.1 cm (95% CI: 11.9, 12.4 cm).
The probability of matching a donor and a recipient decreases with increasing true lung height difference.
Discussion
The use of single CXR lung heights is imprecise for the purpose of donor-recipient size matching for lung transplantation. Within individual variability and the double need for measurements in the donor and the recipient resulting in error propagation are largely responsible for the lack of precision. Between subject variability and rater bias contribute to a smaller extent.
Contemporary cohorts have highlighted the importance of size matching with worse outcomes in cases of size discrepancy (3,4,7,21-23). In a series of studies, Eberlein et al. (3,4,21-23) found that a donor to recipient predicted TLC ratio >1 was associated with improved survival, reduced risk of chronic lung allograft dysfunction and had lower resource utilization overall. The 2019 International Society of Heart Lung Transplantation Registry report focused on size matching (8). Using donor to recipient height differences as a surrogate for TLC, they analyzed 69,200 lung transplantation procedures. The highest mortality at 1 and 5 years was noted in patients receiving smaller lungs and when the donor-recipient height difference was ≤−15 cm (8). These findings emphasize the deleterious effects of transplanting smaller lungs for the size of the recipient.
Oversizing donor lungs can also lead to adverse outcomes. Oversized donor grafts are responsible for all the lung size-reduction procedures during transplantation surgeries and cause 50% of the delayed chest closures (24,25). In a cohort study from Spain, survival at 1 and 5 years was lower in the group of patients requiring any type of allograft reduction surgery (7). Using CXR lung height measured from the apex of the lung to the ipsilateral costophrenic angle, a donor-recipient ratio of >1 was associated with an increased risk of severe primary graft dysfunction and need for lung size reduction (6).
These results highlight the association of predicted TLC and CXR lung heights with outcomes at the population level. At the individual level they both fail to establish accurate size relationships due to their lack of precision. Predictive TLC equations consider sex and age but TLC (12) is dependent on many other factors such as genetic and epigenetic influences, preterm birth, early childhood infections, malnutrition and other noxious exposures (26-28). These factors can’t currently be accounted for reliably and are responsible for the predictions’ wide confidence intervals. The precision of these equations has not improved over the past 50 years and it should not be expected to improve (12). Predictive TLC equations were conceived to differentiate disease states from health, not to be precise. They allow the gross description of relationships between size and outcomes but may not the right tool for personalized size matching.
In the case of CXR lung heights, a simple solution that could be implemented in any setting is the use of mean CXR lung heights across multiple CXRs. Within subject variability—different lung heights in different CXRs taken for the same patient—was the major contributor to the imprecision of individual CXR measurements in our study. This variability can be overcome by averaging multiple measurements (16). Previous studies using double exposure CXR (full inspiration and expiration) found an average diaphragmatic excursion of around 6 cm (14), very close to the range of CXR lung height error in our analysis. We did not make assumptions about the CXR timing in relation to the respiratory cycle, the quality of the inspiratory effort or the radiographic technique. A combination of the three is likely responsible for the observed differences.
Our study has several limitations. Both donors and recipients were selected at random and independent of each other. As a result, we do not know if any of the donors were appropriately accepted or rejected based on size and we do not have data on adverse outcomes related to these actions. However, this was not the goal of our analysis. Our goal was to evaluate the precision of CXR lung heights as a tool for size matching. For this reason, we do not describe an ideal lung height difference between donors and recipients. Future studies using the mean CXR lung height are needed to answer this question.
The average number of CXRs in our study was 4 and this was enough to achieve a margin of error for the mean lung height of approximately 1.5 cm. More measurements would decrease this margin of error according to the formula N = (1.96*SD)/desired margin of error.
Two raters measured all the CXRs twice. They are clinicians involved in clinical lung transplantation and not radiologists. This reflects our local practice. Their measurements were biased from each other by approximately 0.25 cm. Although this bias could be addressed through continued training, the results of the analysis using a single rater and effectively eliminating inter-rater bias, were not substantially different.
Finally, the CXR lung heights are only measuring one dimension, but the lungs are three-dimensional structures. This results in the apparent incongruency of the right lung being shorter on average than the left lung (20 vs. 22 cm) even though its volume is usually larger. A shorter but wider or/and deeper structure can have a larger volume and the relationship between lung height and volume is different for the right and left lungs for this reason. Quantitative computed tomography could overcome this limitation. However, in clinical practice it will likely be subject to errors in measurement similar to those observed in our study (29).
In conclusion, isolated lung height measurements from CXRs are inaccurate for the purpose of donor-recipient size-matching. Error propagation stemming from the need to measure both the donor and the recipient further impedes size-matching. Average lung height measurements across multiple CXRs are more precise and should be validated against clinical outcomes before their implementation in clinical practice.
Acknowledgments
Funding: This research was supported by the Washington University Institute of Clinical and Translational Sciences Grant UL1TR002345 from the National Center for Advancing Translational Sciences (NCATS) of the National Institutes of Health (NIH). The content is solely the responsibility of the authors and does not necessarily represent the official view of the NIH.
Footnote
Reporting Checklist: The authors have completed the STROBE and GRRAS reporting checklists. Available at https://jtd.amegroups.com/article/view/10.21037/jtd-21-1755/rc
Data Sharing Statement: Available at https://jtd.amegroups.com/article/view/10.21037/jtd-21-1755/dss
Peer Review File: Available at https://jtd.amegroups.com/article/view/10.21037/jtd-21-1755/prf
Conflicts of Interest: All authors have completed the ICMJE uniform disclosure form (available at https://jtd.amegroups.com/article/view/10.21037/jtd-21-1755/coif). DK serves as an unpaid editorial board member of Journal of Thoracic Disease. RVG reports that this research was supported by the Washington University Institute of Clinical and Translational Sciences Grant UL1TR002345 from the National Center for Advancing Translational Sciences (NCATS) of the National Institutes of Health (NIH). The content is solely the responsibility of the authors and does not necessarily represent the official view of the NIH. MW reports receiving salary support from Grant UL1TR002345 from the National Center for Advancing Translational Science NCATS of the National Institute of Health (NIH). GFM is the Medical Director at Mid America Transplant. DEB reports receiving research funding from Mid-America Transplant. RH reports receiving research funding from Bristol Myers Squibb and Mallinkrodt, gent funding from Mid America Transplant and personal fees from Transmedics, CareDx, Thevavance, and Vectura. The other authors have no conflicts of interest to declare.
Ethical Statement: The authors are accountable for all aspects of the work in ensuring that questions related to the accuracy or integrity of any part of the work are appropriately investigated and resolved. The study was conducted in accordance with the Declaration of Helsinki (as revised in 2013). The Washington University School of Medicine Institutional Review Board reviewed the protocol and waived the need for informed consent (IRB No. 202012069).
Open Access Statement: This is an Open Access article distributed in accordance with the Creative Commons Attribution-NonCommercial-NoDerivs 4.0 International License (CC BY-NC-ND 4.0), which permits the non-commercial replication and distribution of the article with the strict proviso that no changes or edits are made and the original work is properly cited (including links to both the formal publication through the relevant DOI and the license). See: https://creativecommons.org/licenses/by-nc-nd/4.0/.
References
- Orens JB, Boehler A, de Perrot M, et al. A review of lung transplant donor acceptability criteria. J Heart Lung Transplant 2003;22:1183-200. [Crossref] [PubMed]
- Christie JD, Kotloff RM, Pochettino A, et al. Clinical risk factors for primary graft failure following lung transplantation. Chest 2003;124:1232-41. [Crossref] [PubMed]
- Eberlein M, Permutt S, Chahla MF, et al. Lung size mismatch in bilateral lung transplantation is associated with allograft function and bronchiolitis obliterans syndrome. Chest 2012;141:451-60. [Crossref] [PubMed]
- Eberlein M, Reed RM, Bolukbas S, et al. Lung size mismatch and primary graft dysfunction after bilateral lung transplantation. J Heart Lung Transplant 2015;34:233-40. [Crossref] [PubMed]
- Ganapathi AM, Mulvihill MS, Englum BR, et al. Transplant size mismatch in restrictive lung disease. Transpl Int 2017;30:378-87. [Crossref] [PubMed]
- Li D, Weinkauf J, Hirji A, et al. Chest X-ray Sizing for Lung Transplants Reflects Pulmonary Diagnosis and Body Composition and Is Associated With Primary Graft Dysfunction Risk. Transplantation 2021;105:382-9. [Crossref] [PubMed]
- Montoya P, Bello I, Ascanio F, et al. Graft reduction surgery is associated with poorer outcome after lung transplantation: a single-centre propensity score-matched analysis. Eur J Cardiothorac Surg 2021;60:1308-15. [Crossref] [PubMed]
- Chambers DC, Cherikh WS, Harhay MO, et al. The International Thoracic Organ Transplant Registry of the International Society for Heart and Lung Transplantation: Thirty-sixth adult lung and heart-lung transplantation Report-2019; Focus theme: Donor and recipient size match. J Heart Lung Transplant 2019;38:1042-55. [Crossref] [PubMed]
- Lung function testing: selection of reference values and interpretative strategies. American Thoracic Society. Am Rev Respir Dis 1991;144:1202-18. [Crossref] [PubMed]
- HEPPER NG. FOWLER WS, HELMHOLZ HF Jr. Relationship of height to lung volume in healthy men. Dis Chest 1960;37:314-20. [PubMed]
- Stocks J, Quanjer PH. Reference values for residual volume, functional residual capacity and total lung capacity. ATS Workshop on Lung Volume Measurements. Official Statement of The European Respiratory Society. Eur Respir J 1995;8:492-506. [Crossref] [PubMed]
- Hall GL, Filipow N, Ruppel G, et al. Official ERS technical standard: Global Lung Function Initiative reference values for static lung volumes in individuals of European ancestry. Eur Respir J 2021;57:2000289. [Crossref] [PubMed]
- Gamsu G, Shames DM, McMahon J, et al. Radiographically determined lung volumes at full inspiration and during dynamic forced expiration in normal subjects. Invest Radiol 1975;10:100-8. [Crossref] [PubMed]
- Hurtado A, Fray WW. Studies of total pulmonary capacity and its sub-divisions. II. Correlation with physical and radiological measurements. J Clin Invest 1933;12:807-23. [Crossref] [PubMed]
- Taylor J. An Introduction to Error Analysis. 2nd Edition. Sausalito: 1997.
- Bland JM, Altman DG. Agreement between methods of measurement with multiple observations per individual. J Biopharm Stat 2007;17:571-82. [Crossref] [PubMed]
- von Elm E, Altman DG, Egger M, et al. The Strengthening the Reporting of Observational Studies in Epidemiology (STROBE) statement: guidelines for reporting observational studies. J Clin Epidemiol 2008;61:344-9. [Crossref] [PubMed]
- Kottner J, Audigé L, Brorson S, et al. Guidelines for Reporting Reliability and Agreement Studies (GRRAS) were proposed. J Clin Epidemiol 2011;64:96-106. [Crossref] [PubMed]
- Olofsen E, Dahan A, Borsboom G, et al. Improvements in the application and reporting of advanced Bland-Altman methods of comparison. J Clin Monit Comput 2015;29:127-39. [Crossref] [PubMed]
- Bland JM, Altman DG. Statistical methods for assessing agreement between two methods of clinical measurement. Lancet 1986;1:307-10. [Crossref] [PubMed]
- Eberlein M, Reed RM, Maidaa M, et al. Donor-recipient size matching and survival after lung transplantation. A cohort study. Ann Am Thorac Soc 2013;10:418-25. [Crossref] [PubMed]
- Eberlein M, Reed RM, Bolukbas S, et al. Lung size mismatch and survival after single and bilateral lung transplantation. Ann Thorac Surg 2013;96:457-63. [Crossref] [PubMed]
- Eberlein M, Reed RM, Permutt S, et al. Parameters of donor-recipient size mismatch and survival after bilateral lung transplantation. J Heart Lung Transplant 2012;31:1207-1213.e7. [Crossref] [PubMed]
- Shigemura N, Orhan Y, Bhama JK, et al. Delayed chest closure after lung transplantation: techniques, outcomes, and strategies. J Heart Lung Transplant 2014;33:741-8. [Crossref] [PubMed]
- Rafiroiu S, Hassouna H, Ahmad U, et al. Consequences of Delayed Chest Closure During Lung Transplantation. Ann Thorac Surg 2020;109:277-84. [Crossref] [PubMed]
- Adam M, Schikowski T, Carsin AE, et al. Adult lung function and long-term air pollution exposure. ESCAPE: a multicentre cohort study and meta-analysis. Eur Respir J 2015;45:38-50. [Crossref] [PubMed]
- Morrisey EE, Cardoso WV, Lane RH, et al. Molecular determinants of lung development. Ann Am Thorac Soc 2013;10:S12-6. [Crossref] [PubMed]
- Shaheen SO, Barker DJ, Shiell AW, et al. The relationship between pneumonia in early childhood and impaired lung function in late adult life. Am J Respir Crit Care Med 1994;149:616-9. [Crossref] [PubMed]
- Lee JS, Lee SM, Seo JB, et al. Clinical utility of computed tomographic lung volumes in patients with chronic obstructive pulmonary disease. Respiration 2014;87:196-203. [Crossref] [PubMed]


