
Hemodynamic study of the effect of the geometric height of leaflets on the performance of the aortic valve under aortic valve reconstruction
Introduction
Aortic valve disease has become a serious public health problem (1). Although aortic valve replacement is the gold standard treatment for patients, the duration of the bioprosthetic valve (2) and the need for lifelong anticoagulation for the mechanical valve (3) still limit the application of aortic valve replacement. Aortic valve reconstruction, which involves reconstructing the aortic leaflets using pericardium, has attracted more and more attention as a novel surgical approach. Since bovine pericardium or autologous pericardium is used as valve leaflet material for aortic valve reconstruction, patients do not need to receive special anticoagulation therapy after surgery. For instance, Ozaki et al. proposed technology that uses autologous pericardium to reconstruct the aortic leaflets (4). Ricciardi et al. reported that the aortic valve reconstruction technique could achieve optimal results for younger and less fragile patients (5). Subsequently, Sivalingam et al. presented their experience with aortic valve reconstruction of a single leaflet using the aortic valve neocuspidization technique for patients with aortic regurgitation (AR) associated with doubly committed subarterial ventricular septal defects (6). Similarly, Marathe et al. reported that single-leaflet aortic valve leaflet reconstruction utilizing the Ozaki technique had promising early results and can be considered in patients when there are acceptable native leaflets (7). Recently, Sheng et al. reported that aortic valve reconstruction with bovine pericardium is feasible, and could achieve good early and mid-term results (8). Similarly, Wiggins et al. reported that aortic leaflet reconstruction is feasible for the treatment of aortic valve disease (9). Although aortic valve reconstruction has been proven to have a good effect, the design of the geometric parameters of the reconstructed leaflet still mainly depends on the experience of doctors.
The biomechanical influence of the geometric parameters of leaflets on the performance of the aortic valve has been widely studied. Marom et al. investigated the influence of the ratio of the sinotubular junction (STJ) diameter to the aortic annulus diameter on the hemodynamics of the aortic root (10). Similarly, Hammer et al. employed the finite element approach to study how pericardial leaflet grafts of various sizes interacted with 2 native leaflets when the valve was closed (11). Subsequently, Gaetano et al. investigated the influence of leaflet thickness on the closing performance of the aortic valve using the structural finite element model (12). Ghasemi Pour et al. studied the hemodynamics of blood flow through a normal and stenotic aortic valve in 2 relaxation and exercise conditions using a three-dimensional fluid-structure interaction (FSI) method (13). Similarly, Li et al. investigated the relationship between local mechanical stimuli and regional aortic tissue degeneration using FSI analysis in patients with bicuspid aortic valve (BAV) disease (14). Lavon et al. proposed a computational modeling approach of both the calcification progression in BAV and its biomechanical response incorporating FSI simulations during disease progression (15). Although the above studies have provided much useful information, the effect of the geometric height (gH) of the leaflet on the performance of the aortic valve, especially on the opening performance of the aortic valve in aortic valve reconstruction, is still unclear. Moreover only Li et al. studied (16) the effects of the gH of the leaflets on the performance of the aortic valve by using structural mechanics calculation. As this study ignored interaction between the aortic leaflets and the blood flow, the results cannot provide a comprehensive assessment of the valve's opening or closing performance.
In order to solve this problem, a new geometric parameter of leaflets, namely height ratio (HR), which is the ratio of the commissure height (comH) of the leaflet to the gH of the leaflet, was designed. Three types of leaflets with different HRs (0.8, 1.0, and 1.2) were designed. To study the influence of the HR of leaflets on the performance of the aortic valve, the FSI model was established. The dynamic characteristics, stress distribution, and effective orifice area (EOA) of the aortic valve and flow pattern were calculated as the indicators.
Methods
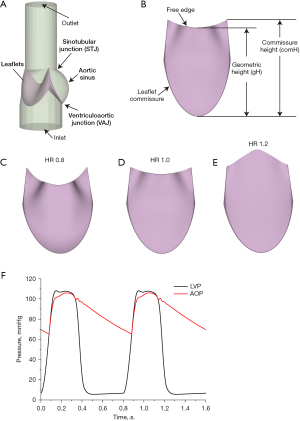
Description of the geometric model
The geometric model used in this study was designed according to a previous study (17). The model consists of the aortic sinus, a part of the ascending aorta, and the leaflets (Figure 1A). The leaflets are placed in the aortic sinus, between the STJ and the ventriculoaortic junction (VAJ). In order to eliminate the effects of the boundary condition on the accuracy of numerical simulation, the outlet and inlet of the model were extended. Figure 1B illustrates the schematic diagram of the leaflet. The leaflet commissure is the surface, where the leaflets contact the aortic sinus. The comH is the distance between the STJ and VAJ. The gH of the leaflets is the distance between the middle point of the free edge of the leaflet and the middle point of the leaflet commissure (Figure 1B). In order to evaluate the height of the leaflets, a new geometric factor, namely HR, is proposed here. HR is defined as the ratio of the gH to the comH, as per Eq. [1],
Where HR represents the height ratio of the leaflet, gH denotes the geometric height of the leaflets (unit mm), and comH is the commissure height of the leaflets (unit mm). HR is actually the normalization of gH with respect to comH.
In the clinical practice, the geometric parameters of the reconstructed leaflet were determined by the geometric size of the aortic sinus and the native leaflets. The widths of the leaflets were determined by the size of the sinotubular junction. The surgeon would measure the circumference of the patient's sinotubular junction, and then 1/3 of the sinotubular perimeter would be used as the width of the reconstructed leaflet. Similarly, the commissure height of the leaflets would be determined by the height of the aortic sinus.
In order to evaluate the effects of HR on the performance of the aortic valve, 3 types of leaflets with different HRs were designed as shown from Figure 1C-1E. According to the value of the HR, the 3 types of leaflets were named HR_0.8, HR_1.0, and HR_1.2, respectively. The details of the 3 types of leaflets are listed in Table 1. The range of HR used in this study could ensure that the leaflet does not have regurgitation during diastole, and the valve leaflet will not completely cover the aortic sinus during systole to ensure coronary perfusion. According to our previous preliminary study, when HR is less than 0.8, the aortic valve insufficiency would be observed during the diastolic phase of the left ventricle. In addition, when the HR is greater than 1.2, the valve leaflets would cover the aortic sinus during the systolic phase, which would prevent blood flow into the coronary arteries.
Table 1
| Name of leaflets | Value of the HR |
|---|---|
| HR_0.8 | 0.8 |
| HR_1.0 | 1.0 |
| HR_1.2 | 1.2 |
HR, height ratio.
The boundary condition
In this study, the boundary conditions of the inlet and outlet of the model were derived from the lumped parameter model, reported in a previous study (18). The model consists of the pulmonary circulation system, left atrium, left ventricle, systemic circulation, right atrium, and right ventricle. The aortic pressure (AOP) and the left ventricular pressure (LVP) were calculated as the outlet and inlet boundary condition, shown as in Figure 1F. During the simulation, the heart rate was set to 75 bpm, in which the systolic phase was 0.3 s and the diastolic phase was 0.5 s.
Description of the FSI approach
The details of the FSI approach used in this study were reported in a previous study (17), and only a simple explanation is given here. The FSI approach combined the lattice Boltzmann method (LBM) and the finite element method (FEM). The blood flow pattern was calculated by applying the LBM to simulate the truncation of the fluid domain after the aortic valve fully closed. According to the theory of the LBM, the density, momentum, pressure, and shear stress tensor of the blood are governed by Eqs. [2-5]
Where ρ is the blood density, ρu denotes the blood momentum, ei is the discrete velocity model, fi denotes the set of populations, p denotes the blood pressure, σxy is the shear stress tensor of blood, and Cs denotes the speed of sound of the blood, which is associated with the incompressibility of the blood.
To calculate the biomechanical information of the leaflets, the FEM was employed. According to previous studies (17,19), the isotropic, hyperelastic, incompressible, second-order Ogden function was used to mimic the biomechanical characteristics of the leaflets, which is governed by the Eq. [6],
Where W denotes the strain energy function, represents the principal stretch, and µi and αi denote the material parameters α1=67.74, α2=27.47, µ1=19.58 kPa, and µ2=260.56 kPa. In addition, the density of the leaflets was set to be 1100 kg/m3.
In this work, the 10-node quadratic tetrahedral (C3D10) element was employed to discretize the leaflets to achieve second order accuracy. According to a previous study (16), 0.5 mm was chosen as the element size of the leaflets. The number of elements of the 3 types of leaflets was HR_0.8: 20,128, HR_1.0: 22,265, and HR_1.2: 26,254. For the blood domain, the element size was set to be 0.3 mm based on the results of the reference (17). The octree lattice structure was employed to discretize the fluid domain to obtain the fourth-order spatial discretization. The number of elements of the fluid domain was about 1.3 million.
In this study, the Abaqus/Explicit solver was employed to calculate the biomechanical states and the deformation of the leaflets. Meanwhile, the commercial software XFlow 2019x was used to calculate the blood flow pattern in the aorta. The Co-simulation Engine was employed to regulate the data transfer between the 2 solvers. In addition, the blood was assumed to be a homogeneous, incompressible, Newtonian fluid, whose density and viscosity were set to be 1,050 kg/m3 and 0.0035 Pa·s, respectively. The time step was set to 1E-5s to capture the deformation of the leaflets. Meanwhile, the aortic wall was assumed as the rigid body to shorten the calculation time.
Biomechanical analysis
To study the dynamic and biomechanical characteristics, the mean stress, radial displacement (RD), EOA, blood flow pattern, and distribution of the wall shear stress (WSS) were calculated.
The mean stress (16) reflects the mean level of the principal stress, governed by Eq. [7]
Where stressm denotes the volume average principal stress of the aortic leaflets, stressi denotes the principal stress on the i th element of the leaflets, and voli is the volume of the i th element.
RD is the factor that reflects the performance of the aortic valve, which is governed by Eq. [8]
Where RDm(t) represents the radial displacement of the middle point of the free edge of the leaflets, xm and zm are the coordinates of the midpoint of the free edge at the time step, and xo and zo represent the initial coordinates of the midpoint of the free edge.
EOA reflects the opening performance of the aortic valve, and is calculated based on Eq. [9]
Where EOA refers to the effective orifice area of the leaflets during the systole phase, Qpeak is the flow rate (mL/s) of the blood through the aortic valve at the peak systole, ΔP denotes the transvalvular pressure gradient (mmHg) at the peak systole, and Cd represents the discharge coefficient, which was equal to 1 in the aorta.
Results
In this study, the dynamic characteristics, stress distribution, EOA of the aortic leaflets, and blood flow pattern in the aortic root were chosen as factors. The fully open time, fully closed (about 450 ms) time, and the midpoint of the rapid valve closing phase (about 375 ms) were selected as the time points. The results are illustrated in Figures 2-5.
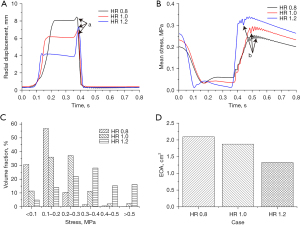
The dynamic characteristics of leaflets
Figure 2 shows the dynamic characteristics of the 3 types of leaflets. Figure 2A shows the changes in RDm of the 3 types of leaflets. It was found that the rapid valve opening time (RVOT) of the 3 types of leaflets gradually reduced along with the decrease of the HR (HR_0.8: 120 ms vs. HR_1.0: 68 ms vs. HR_1.2: 31 ms). In addition, the value of the RDm at the fully open time increased along with the decrease of the HR (HR_0.8: 8 mm vs. HR_1.0: 6 mm vs. HR_1.2: 4 mm). The rapid valve closing times (RVCTs) of the 3 types of leaflets were similar to each other (approximately 75 ms). It is worth noting that during the diastole phase of the cardiac cycle, the value of RDm increased at first and then decreased (region a), which is due to the fact that when the leaflets rapidly close, the free edge of the leaflets bends into the aortic sinus (Figure 4). According to the value of RDm, the bending degree of the free edge increased with the increase of HR. Figure 2B shows the waveform of the mean stress of the leaflets. During the systolic period, the stress of the leaflets was relatively low. Meanwhile, the mean stress level increased with the decrease of the HR. During the diastolic period, with the increase of the pressure difference of the aortic valve, the stress of the 3 types of leaflets gradually increased. After the aortic valve fully closed, the stress level of the leaflets was inversely proportional to the HR of the leaflets (region b). Meanwhile, in the diastolic period, the value of the stress of the 3 types of leaflets fluctuated, resulting from the impact of blood regurgitation during valve closure. This phenomenon is termed “water hammer”, which was reported by a previous study (15). To evaluate the effect of HR on the opening performance of the aortic valve, the EOA is illustrated in Figure 2D. It was observed that the value of the EOA decreased along with the increase of the HR of the leaflets, which means the leaflets with a lower HR had better opening function.
The stress distribution of leaflets
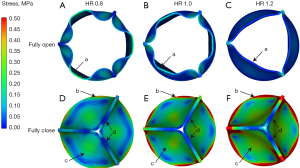
Figure 3 shows the distribution of the principal stress of the leaflets at the fully open time and fully closed time. It was seen that at the fully open time, the leaflets with HR =0.8 achieved the maximum value of geometric orifice area (GOA), while the value of the GOA of the leaflets with HR =1.2 was at the minimum (Figure 3A-3C). In addition, the stress level of the leaflets with HR =0.8 was the highest among the 3 types of leaflets. Moreover, the high stress region was found at the middle part of the free edge of the leaflets with HR ≤1.0 (region a). In contrast, for the leaflets with HR =1.2, the stress level was significantly lower than that of the other 2 types of leaflets, and no obvious high stress region was found at the free edge of the leaflets (Figure 3C, region a). At the fully closed time, all 3 types of leaflets were completely closed and no insufficiency was found. In addition, the distribution of the stress among the leaflets was similar. The high stress region was observed at the leaflet commissure (Figure 3D-3F, region b), while the low stress region was found at the free edge of the leaflets (region c,d). However, the stress level of the leaflets with HR =1.2 was significantly higher than that of the leaflet with HR =0.8 (max stress, HR_0.8: 0.5 MPa, vs. HR_1.0: 1.1 MPa, vs. HR_1.2: 1.8 MPa). To further study the distribution of stress among the leaflets, the volume fraction of different stress ranges at the fully closed time was calculated and illustrated in Figure 2C. The whole stress range was divided into 6 parts. The stress of the leaflet with HR ≤1.0 was mainly concentrated in the low stress region (less than 0.3 MPa), while the stress of the leaflets with HR =1.2 was concentrated in the high stress region (larger than 0.3 MPa).
Figure 4 illustrates the distribution of stress at the midpoint of the rapid valve closing phase. Obvious bending was observed at the leaflets with HR =1.2. Meanwhile, the high stress region was found at the free edge of the leaflet with HR ≤1.0, while the low stress region was at the same position of the leaflet with HR =1.2 (region a). In addition, the high stress area appeared at the joint of the commissure and free edge of the leaflet (region b).
The blood flow pattern and WSS
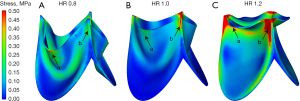
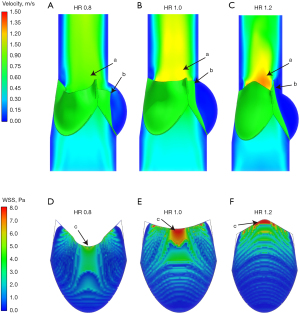
Figure 5 shows the flow pattern in the aortic root and the WSS distribution of the leaflets. Figure 5A-5C show the blood flow patterns of the 3 types of leaflets at the fully open time. The high blood velocity region appeared in the center of the ascending aorta (region a), which is consistent with a previous study (19). Due to the GOA of the leaflets with HR =1.2 being the smallest among the 3 types of leaflets, the value of the blood velocity was the highest (region a) (max velocity HR_0.8: 0.7 m/s vs. HR_1.0: 0.9 m/s vs. HR_1.2: 1.25 m/s). In addition, along with the increase of the HR of the leaflets, the area of low flow velocity near the ascending aortic wall was larger (region b).
Figure 5D-5F illustrate the distribution of WSS at the fully open time. Due to the symmetry of the geometric model, the WSS distribution of one leaflet of each model was calculated. At the fully open time, the blood flow mainly impacted the ventricular side of the leaflets. Hence, the distribution of WSS on the ventricular side of the leaflets is illustrated. It was seen that the high WSS regions of the 3 types of leaflets appeared near the middle part of the free edge of the leaflets (region c). In addition, the WSS level of the leaflets increased along with the increase of the HR of the leaflets (max WSS, HR_0.8: 4 Pa vs. HR_1.0: 7 Pa vs. HR_1.2: 12 Pa).
Discussion
This numerical study was conducted to clarify the effects of the height of leaflets on the biomechanical states of the aortic valve. Although there have been some studies (20,21) on the geometric design of the leaflets in aortic valve reconstruction, the designs are mainly based on the clinical experience of doctors. In addition, most previous studies (16,22) on aortic valve reconstruction focus on the closing performance of the reconstructed leaflets, that is, to prevent aortic insufficiency. To our knowledge, this is the first study on the effects of the height of the leaflets on the biomechanics and the opening function of the aortic valve. Meanwhile, a novel geometric factor, namely HR, was proposed which normalized the quantification of the relationship between the leaflet height and the aortic sinus height. The results demonstrated that there was no AR when the HR was between 0.8 and 1.2. However, with the increase of the HR, the opening function of the aortic valve decreased gradually, while its stress increased.
The dynamic characteristics are an important index to evaluate the function of the aortic valve, which is closely related to the prognosis of patients. Makkar et al. reported that reduced leaflet motion was observed in patients who had a stroke after transcatheter aortic valve (TAV) implantation (23). According to Figure 2A, the RVOT was significantly reduced along with the increase of the HR of the leaflets. There may be 2 reasons for this difference. The first reason is that as the height of the leaflet increases, the opening area decreases at the fully open time. As a result, the RD of the valve will also become smaller. The second reason is that the area of the leaflet increases with the increase of the height of the leaflet. As a result, the hemodynamic force acting on the leaflets increases. Therefore, according to Newton’s second law, the greater the HR of the leaflets, the greater its acceleration at the opening stage, which could also be confirmed by the slope of the RD curve (Figure 2A). The slope of RDm of the leaflets with HR =1.2 was the largest among the 3 types of leaflets. In addition, the EOA of the aortic valve had a negative correlation with the HR of the leaflets. The smaller the EOA, the greater the transvalvular resistance of the aortic valve. Hence, in order to ensure the opening function of the aortic valve, the valve height should be carefully determined and should not be too high.
Stress is considered an important biomechanical factor that affects not only the performance of the aortic valve but also the mechanobiology of the leaflets. For instance, Huang et al. found that interstitial cells express smooth muscle alpha-actin and are considered to respond to mechanical stimuli (24). Recently, Bogdanova et al. reported that mechanical stress triggers the expression of osteogenic genes in aortic valve interstitial cells (25). According to the results of the present study, the stress level and the high stress regions of the leaflets increased with the increase of the HR of the leaflets (Figure 3). Moreover, the high stress volume fraction also gradually reduced along with the decrease of the HR of the leaflets (Figure 2C). This means that the leaflets with a larger HR would be subjected to higher mechanical stress during the diastolic phase, which might be more likely to trigger remodeling. Hence, the doctor should carefully choose the height of the reconstructed leaflets, preventing aortic valve insufficiency while reducing the mechanical stress of the leaflets to avoid valve remodeling.
Besides mechanical stress, the blood flow pattern and WSS are also important hemodynamic factors that closely relate to the remodeling of the aortic valve. For instance, Davies et al. demonstrated that the low shear stress regions at the aortic sinus might cause flow stagnation and increased adhesion of thrombotic and inflammatory cells (26). Similarly, Kassab et al. reported that low WSS reduced endothelium nitric oxide production and nitric oxide synthase, which were atheroprotective and anti-inflammatory (27). Arjunon et al. demonstrated that low and oscillatory shear stress is atheroprone, whereas high shear is atheroprotective (28). From Figure 5, it can be seen that the low velocity region in the aortic sinus and near the ascending aortic wall increased along with the increase of the HR of the leaflets. In addition, when the aortic valve HR was less than 1, obvious blood flow was observed to flow into the aortic sinus (Figure 5, region b). Hence, if the HR of the leaflets can be properly reduced, it may be more beneficial to maintain the normal structure and function of the aortic valve and prevent the calcification of the aortic leaflet.
Limitations
Some limitations need to be explained. Firstly, the geometric models of the leaflets in this study are ideal models, in which the geometric sizes of the 3 leaflets of the models are the same as each other. Although the geometric sizes of the 3 leaflets of one patient are not the same, the results of the present article can still provide useful information for clinical application.
Secondly, the present study only investigated the effects of the height of the leaflets on the aortic valve. There are still many other geometric parameters, including the width of the leaflets, the thickness of the leaflets, the material property, and the suture method. All these factors could affect the biomechanical states and the performance of the reconstructed aortic valve. In the future, we will carry out research on these parameters.
Thirdly, only the deformation of the leaflets was considered, and the aortic sinus was assumed as a rigid body. According to a previous study (7), the deformation of the aortic annulus and aortic sinus will also affect the function of the aortic valve. This simplification might affect the accuracy of the results. In the future, studies involving the deformation of the aortic sinus will be carried out.
Lastly, in the present study, the isotropic hyperelastic constitutive model was employed. The real constitutive model of the leaflets was an anisotropic constitutive model. Although the simplification aims to reduce the cost of the numerical simulation, the effectiveness of this simplification has been proven. Hence, the present study still provides useful information. In the future, research involving the real constitutive model of the bovine pericardium will be carried out.
Conclusions
In this study, the effects of the height of the reconstructed leaflets on the biomechanical states and the performance of the aortic valve were investigated by using a novel FSI approach. A new geometric factor, namely HR, was proposed to quantify the height of the leaflets. Three types of leaflets with different HRs were designed. The results demonstrated that the height of the leaflets could indeed regulate the performance and the biomechanical states of the aortic valve. The RVOT of the 3 types of leaflets gradually reduced along with the decrease of the HR (HR_0.8: 120 ms vs. HR_1.0: 68 ms vs. HR_1.2: 31 ms), however, the RD of the leaflet at the fully open time increased along with the decrease of the HR of the leaflets (HR_0.8: 8 mm vs. HR_1.0: 6 mm vs. HR_1.2: 4 mm). In addition, the stress level of the leaflets also increased with the increase of the height of the leaflets (max stress, HR_0.8: 0.5 MPa, vs. HR_1.0: 1.1 MPa, vs. HR_1.2: 1.8 MPa). Similarly, the low velocity region near the ascending aortic wall and the WSS level on the ventricular side of the leaflets also increased along with the increase of the HR of the leaflets. In short, the height of the leaflets mainly affects the opening function of the reconstructed aortic valve. The strategies of aortic valve reconstruction should be different for patients with different ages. The HR of the reconstructed leaflets for adults should be less than 1.0 to balance the opening function and closing function of the aortic valve.
Acknowledgments
Funding: This study was partly funded by the National Natural Science Foundation of China (Nos. 61931013, 82171886, 81701644, and 11832003), the Key Research and Development Program of Shanxi province (No. 201903D321149), Youth Top Talent Training Program (No. CIT&TCD201904025), and Key Research and Development Program (No. 2017YFC0111104).
Footnote
Conflicts of Interest: All authors have completed the ICMJE uniform disclosure form (available at https://jtd.amegroups.com/article/view/10.21037/jtd-22-425/coif). The authors have no conflicts of interest to declare.
Ethical Statement: The authors are accountable for all aspects of the work in ensuring that questions related to the accuracy or integrity of any part of the work are appropriately investigated and resolved.
Open Access Statement: This is an Open Access article distributed in accordance with the Creative Commons Attribution-NonCommercial-NoDerivs 4.0 International License (CC BY-NC-ND 4.0), which permits the non-commercial replication and distribution of the article with the strict proviso that no changes or edits are made and the original work is properly cited (including links to both the formal publication through the relevant DOI and the license). See: https://creativecommons.org/licenses/by-nc-nd/4.0/.
References
- Nkomo VT, Gardin JM, Skelton TN, et al. Burden of valvular heart diseases: a population-based study. Lancet 2006;368:1005-11. [Crossref] [PubMed]
- Vahanian A, Alfieri O, Andreotti F, et al. Guidelines on the management of valvular heart disease (version 2012): the Joint Task Force on the Management of Valvular Heart Disease of the European Society of Cardiology (ESC) and the European Association for Cardio-Thoracic Surgery (EACTS). Eur J Cardiothorac Surg 2012;42:S1-44. [Crossref] [PubMed]
- Lim WY, Lloyd G, Bhattacharyya S. Mechanical and surgical bioprosthetic valve thrombosis. Heart 2017;103:1934-41. [PubMed]
- Ozaki S, Kawase I, Yamashita H, et al. Aortic valve reconstruction using self-developed aortic valve plasty system in aortic valve disease. Interact Cardiovasc Thorac Surg 2011;12:550-3. [Crossref] [PubMed]
- Ricciardi G, Biondi R, Tamagnini G, et al. Aortic Valve Reconstruction with Ozaki Technique. Braz J Cardiovasc Surg 2022;37:118-22. [PubMed]
- Sivalingam S, Haranal M, Pathan IH. Aortic valve neocuspidization for aortic regurgitation associated with ventricular septal defect. Interact Cardiovasc Thorac Surg 2022;34:315-21. [Crossref] [PubMed]
- Marathe SP, Chávez M, Sleeper LA, et al. Single-Leaflet Aortic Valve Reconstruction Uti-lizing the Ozaki Technique in Patients With Congenital Aortic Valve Disease. Semin Thorac Cardiovasc Surg 2021; Epub ahead of print. [Crossref] [PubMed]
- Sheng W, Zhao G, Chao Y, et al. Aortic Valve Replacement with Bovine Pericardium in Patients with Aortic Valve Regurgitation. Int Heart J 2019;60:1344-9. [Crossref] [PubMed]
- Wiggins LM, Mimic B, Issitt R, et al. The utility of aortic valve leaflet reconstruction techniques in children and young adults. J Thorac Cardiovasc Surg 2020;159:2369-78. [Crossref] [PubMed]
- Marom G, Halevi R, Haj-Ali R, et al. Numerical model of the aortic root and valve: optimization of graft size and sinotubular junction to annulus ratio. J Thorac Cardiovasc Surg 2013;146:1227-31. [Crossref] [PubMed]
- Hammer PE, Chen PC, del Nido PJ, et al. Computational model of aortic valve surgical repair using grafted pericardium. J Biomech 2012;45:1199-204. [Crossref] [PubMed]
- Gaetano F, Bagnoli P, Zaffora A, et al. A Newly Developed Tri-Leaflet Polymeric Heart Valve Prosthesis. J Mech Med Biol 2015; [Crossref] [PubMed]
- Ghasemi Pour MJ, Hassani K, Khayat M, et al. Modeling of aortic valve stenosis using fluid-structure interaction method. Perfusion 2022;37:367-76. [Crossref] [PubMed]
- Li F, Wang S, Gao Q, et al. Vessel structural stress mediates aortic media degeneration in bicuspid aortopathy: New insights based on patient-specific fluid-structure interaction analysis. J Biomech 2021;129:110805. [Crossref] [PubMed]
- Lavon K, Morany A, Halevi R, et al. Progressive Calcification in Bicuspid Valves: A Cou-pled Hemodynamics and Multiscale Structural Computations. Ann Biomed Eng 2021;49:3310-22. [Crossref] [PubMed]
- Li H, Pan Y, Qiao A, et al. Influence of valve height on the opening/closure performance of transplanted aortic valve. Sheng Wu Yi Xue Gong Cheng Xue Za Zhi 2019;36:199-205. [PubMed]
- Gao B, Zhang Q, Chang Y. Hemodynamic effects of support modes of LVADs on the aortic valve. Med Biol Eng Comput 2019;57:2657-71. [Crossref] [PubMed]
- Zhang Y, Gao B, Yu C. The hemodynamic effects of the LVAD outflow cannula location on the thrombi distribution in the aorta: A primary numerical study. Comput Methods Programs Biomed 2016;133:217-27. [Crossref] [PubMed]
- Mao W, Li K, Sun W. Fluid-Structure Interaction Study of Transcatheter Aortic Valve Dynamics Using Smoothed Particle Hydrodynamics. Cardiovasc Eng Technol 2016;7:374-88. [Crossref] [PubMed]
- Rankin JS, Nöbauer C, Crooke PS, et al. Techniques of autologous pericardial leaflet replacement for aortic valve reconstruction. Ann Thorac Surg 2014;98:743-5. [Crossref] [PubMed]
- Grousson N, Lim KH, Lim HS, et al. Ventriculo-aortic junction in human root. A geometric approach. J Biomech 2007;40:2167-73. [Crossref] [PubMed]
- Loureiro-Ga M, Veiga C, Fdez-Manin G, et al. A biomechanical model of the pathological aortic valve: simulation of aortic stenosis. Comput Methods Biomech Biomed Engin 2020;23:303-311. [Crossref] [PubMed]
- Makkar RR, Fontana G, Søndergaard L. Possible Subclinical Leaflet Thrombosis in Bioprosthetic Aortic Valves. N Engl J Med 2016;374:1591-2. [PubMed]
- Huang HY, Liao J, Sacks MS. Insitu deformation of the aortic valve interstitial cell nucleus under diastolic loading. J Biomech Eng 2007;129:880-89. [Crossref] [PubMed]
- Bogdanova M, Kostina A, Zihlavnikova Enayati K, et al. Inflammation and Mechanical Stress Stimulate Osteogenic Differentiation of Human Aortic Valve Interstitial Cells. Front Physiol 2018;9:1635. [Crossref] [PubMed]
- Davies PF. Endothelial mechanisms of flow-mediated athero-protection and susceptibility. Circ Res 2007;101:10-2. [Crossref] [PubMed]
- Kassab GS, Navia JA. Biomechanical considerations in the design of graft: the homeostasis hypothesis. Annu Rev Biomed Eng 2006;8:499-535. [Crossref] [PubMed]
- Arjunon S, Rathan S, Jo H, et al. Aortic valve: mechanical environment and mechanobiology. Ann Biomed Eng 2013;41:1331-46. [Crossref] [PubMed]
(English Language Editor: C. Betlazar-Maseh)


