
The accuracy of simplified calculation of mechanical power: a simulation study
Highlight box
Key findings
• The algebraic formulas may introduce considerably large bias under the presented lung conditions. In clinical practice, the trend rather than the value of mechanical power (MP) calculated by formulas should require more attention.
What is known and what is new?
• Although the algebraic formulas would have different accuracy under volume- or pressure-controlled ventilation, they were reported to be accurate.
• The bias introduced by algebraic formulas could be considerably significant. And we are the first to find that in volume- and pressure-controlled ventilation, MPs calculated by algebraic formulas seem to be larger than those of the gold standard in very severe ARDS patients (Crs <25 mL/cmH2O).
What is the implication, and what should change now?
• In clinical practice, the trend rather than the value of MP calculated by formulas should require more attention.
Introduction
The acute respiratory distress syndrome (ARDS) affects approximately 3 million patients annually, accounting for 10% of intensive care unit (ICU) admissions (1). Despite decades of research, treatment options for ARDS are limited, with high mortality ranging from 35% to 46% for severe patients (1). Supportive care with mechanical ventilation (MV) remains the mainstay of management to maintain respiratory function and to reduce work of breathing in ARDS patients (2). However, the mechanical forces generated during the MV by the interaction between the ventilator and the respiratory system can also damage the lung, which is called ventilator-induced lung injury (VILI) (3-5). VILI represents the unwanted result of a complex interplay among various mechanical forces that act on lung structures, which may introduce volutrauma and barotrauma. Many factors including tidal volume (Vt), driving pressure (ΔP), airflow (V’), respiratory rate (RR) and positive end-expiratory pressure (PEEP) contribute to VILI (3), especially, the driving pressure and RR (6).
Recently, the mechanical power (MP), which is the amount of energy per unit of time generated by the MV and released on the respiratory system, unifying the mechanical drivers of VILI, has been proposed as a determinant of the VILI pathogenesis (7-9). The recognition that MP represents a conjunction of parameters predisposing to VILI is an important step toward better care of critically ill patients. The reference standard method is based on an analysis of quasi-static PV curves of the respiratory system (the geometric method) (8). Unfortunately, the calculation is rather cumbersome at beside. In order to facilitate the estimation of MP, the original equation was simplified in different forms (the algebraic formulas) (10,11). However, the simplification requires a series of prerequisites that in reality could not be fulfilled. The accuracy of the algebraic formulas is remained unknown, particularly in moderated and severe ARDS. In the algebraic formulas, compliance is assumed constant throughout the entire breath, which might not be the case in moderated and severe ARDS (12).
The aim of the present study was to compare the accuracy and application of different formulas calculating MP. A lung simulator was used to simulate pulmonary compliance variations. We present this article in accordance with the STROBE reporting checklist (available at https://jtd.amegroups.com/article/view/10.21037/jtd-22-1409/rc).
Methods
Study design
We performed a prospective bench study using a lung simulator (TestChest®, ORGANIS GmbH, Switzerland) to assess the accuracy of the algebraic formulas when calculating MP under different ventilation modes. The TestChest® is a full physiologic artificial lung that can simulate the human respiratory and circulatory systems’ responses of the healthy and pathological adult lung (13). A male patient with the height of 175 cm, with a predicted body weight of 70 kg, and tidal volume of 6 mL/kg, was simulated.
MP calculation
The amount of energy transferred from the ventilator to the patient is measured in joules (J), while power is defined as the amount of energy transferred per unit of time (J/min). The reference standard geometric method can be validated using the area enclosed by the dynamic pressure-volume loop, which was calculated offline with a customized software developed with Matlab (The MathWorks Inc., Natick, USA). In order to calculate MP from the variables measured at the bedside, a simplified equation (Eq. [1]) was proposed (7), which was derived under volume controlled (VC) mode when inspiratory flow is constant.
where 0.098 is a conversion factor to J/min, MP is the mechanical power, RR is the respiratory rate, Vt represents the tidal volume in liter, Ppeak denotes the peak pressure, Pplat is the plateau pressure and PEEP is positive end-expiratory pressure in cmH2O. Eq. [1] can be further transformed to other forms (Eqs. [2] and [3]) (7, 11).
where Crs is the respiratory system compliance L/cmH2O, I:E denotes the inspiratory-to-expiratory time, Raw represents the airway resistance in cmH2O/L/s.
When ventilated with pressure controlled (PC) mode, the algebraic formulas of MP can be calculated by the complicated equation (Eq. [4]) and the simple forms (Eqs. [5] and [6]) (10,14).
where ∆Pinsp is the inspiratory pressure in cmH2O, Tslope is the inspiratory pressure rise time in s, Tinsp is the inspiratory time in s.
Parameter settings
In the study, a simulated lung was ventilated by CARESCAPE R860 (GE Healthcare, Chicago, US). Using the TestChest system software, the parameters, including compliance and airway resistance, were set to simulate various ARDS lungs. Ventilator was also set to different modes (VC and PC) with various parameters (RR, Tinsp, PEEP) to ventilate the simulated lung of ARDS. Vt was set to 420 mL during VC and driving pressure was titrated to result in a similar Vt during PC. For the lung simulator, Raw was fixed to 5 cmH2O/L/s. Crs below lower inflation point (LIP) or above upper inflation point (UIP) was set to 10 mL/cmH2O. Other parameter settings for the lung simulator and ventilator in different scenarios were summarized in Table 1. The variables explained in the Eqs. [1-6] were measured in each condition. MP was calculated according the above formulas. Mean values were computed over five consecutive breaths.
Table 1
| Fixed ventilator parameters | Fixed simulator parameters | Changing parameter |
|---|---|---|
| Scenario 1 | ||
| PEEP 5 cmH2O | – | Crs between LIP & UIP: 10–45 with a step of 5 mL/cmH2O |
| RR 20/min | ||
| Tinsp 1 s | ||
| Scenario 2 | ||
| RR 20/min | Crs between LIP & UIP: 30 mL/cmH2O | PEEP: 5–15 with a step of 2 cmH2O |
| Tinsp 1 s | ||
| Scenario 3 | ||
| PEEP 5 cmH2O | Crs between LIP & UIP: 30 mL/cmH2O | Tinsp: 0.9–1.4 with a step of 0.1 s |
| RR 20/min | ||
| Scenario 4 | ||
| PEEP 5 cmH2O | Crs between LIP & UIP: 30 mL/cmH2O | RR: 12 to 24 with a step of 4/min |
| Tinsp 1 s | ||
Each scenario was adapted to VCV and PCV. PEEP, positive end-expiratory pressure; RR, respiratory rate; Crs, respiratory system compliance; LIP, lower inflection point; UIP, upper inflection point.
Statistical analysis
The data were analyzed with MATLAB (R2015a, The MathWorks Inc., Natick, USA). Lilliefors test was used to check the distribution. For non-normal distribution, data were presented as median (interquartile range). The MPs measured by the geometric method and calculated with the simplified algebraic formulae were compared using the Bland-Altman technique, Pearson’s linear correlation and Wilcoxon signed rank test. A P value <0.05 was considered statistically significant.
Results
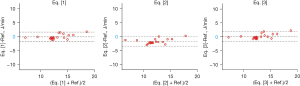
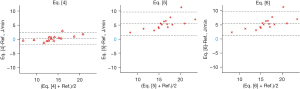
The performances of the formulas were different, although the derived MP were significantly correlated with that derived from the reference method (Ref) (R2>0.80, P<0.001). Under volume-controlled ventilation, medians of MP calculated with Eqs. [1] and [3] were similar to the geometric method. The mean difference for Eq. [1] vs. Ref was −0.13 J/min, with upper and lower limits of agreement 1.60 and −1.85 J/min. The mean difference for Eq. [3] vs. Ref. was 0.06 J/min, with upper and lower limits of agreement 1.78 and −1.66 J/min. However, MP calculated with Eq. [2] was significantly lower than that with the reference method (P<0.001). The mean difference for Eq. [2] vs. Ref was −1.82 J/min, with upper and lower limits of agreement −3.49 and −0.16 J/min (Table 2, Figure 1, Table S1 and Table S2). Under pressure-controlled ventilation, median of MP calculated with Eq. [4] was similar to the geometric method. The mean difference for Eq. [4] vs. Ref was 0.26 J/min, with upper and lower limits of agreement −1.77 and 2.29 J/min. However, MPs calculated with Eqs. [5] and [6] were significantly higher than that with the reference method (P<0.001). The mean difference for Eq. [5] vs. Ref was 5.41 J/min, with upper and lower limits of agreement 9.58 and 1.24 J/min. The mean difference for Eq. [6] vs. Ref was basically the same with that of Eq. [5] (Table 2, Figure 2, Tables S3,S4).
Table 2
| MP | Algebraic | Median (IQR) | Ref. | P (signed rank) | R2 | Δ/Ref. in % |
|---|---|---|---|---|---|---|
| VC | Eq. [1] | 12.1 (2.8) | 12.7 (1.7) | 0.38 | 0.90§ | 5.0 (5.0) % |
| Eq. [2] | 10.5 (2.5) | <0.001* | 0.89§ | 17.2 (6.1) % | ||
| Eq. [3] | 12.3 (2.7) | 0.72 | 0.91§ | 4.0 (3.4) % | ||
| PC | Eq. [4] | 13.6 (3.3) | 13.3 (2.1) | 0.44 | 0.94§ | 4.9 (2.6) % |
| Eq. [5] | 19.3 (4.1) | <0.001* | 0.82§ | 36.0 (14.7) % | ||
| Eq. [6] | 19.3 (4.1) | <0.001* | 0.82§ | 36.1 (14.8) % |
*, significantly different compared to the MP calculated with the reference method; §, two methods were significantly correlated. MP, mechanical power; VC, volume controlled; PC, pressure controlled; Eq., equation; IQR, interquartile range; Ref., reference method; R, linear correlation coefficient; Δ/Ref., the differences of MP calculated with algebraic formulas and the reference method divided by reference MP.
Discussion
In this study, some of the explored algebraic formulas delivered satisfactory MP values compared to the reference method (Eqs. [1], [3] and [4]). However, the others have significant differences compared to the reference method. The maximum difference was over 70% of the MP value calculated with the reference method. To our best knowledge, this is the first simulation study investigating the algebraic formulas under various conditions.
The algebraic formulas were derived under various assumptions, as discussed in their original studies (7,14). Applications without clarifying the perquisites may lead to significant errors. One of the most common mistakes of applying the algebraic formulas is to mix up pressure- and volume-controlled ventilation. Inspiratory flow during volume-controlled ventilation is approximately constant, which is not the case during pressure-controlled. The corresponding error introduced to MP calculation is unneglectable (6,15,16). Another point that acquires attention is the units of the parameters in the formulas. Typically, the parameter values read from ventilator need to be converted before MP calculation (e.g., tidal volume in milliliter to liter, compliance in mL/cmH2O to L/cmH2O). Failed to convert the units may lead to incorrect results (8). In Eqs. [4] and [5], time constant is required. A previous study claimed to have Crs in mL/cmH2O and Raw in cmH2O∙s∙L-1 (17), which would not have a correct result per se.
Volume-controlled ventilation
During volume-controlled ventilation, Eq. [2] delivered MPs that were in average 17.2% different from the reference values (Table 2) (7). Compared to Eqs. [1] and [3], Eq. [2] has the term of Crs and Raw, which are non-linear in the present study. On the one hand, Crs was overestimated below LIP and beyond UIP, and at the same time, the Crs of TestChest also changed dynamically near the set value with the ventilation setting, but Eq. [2] only used the set value for calculation. On the other hand, Raw was directly derived from the set value of TestChest, it was Raw =5 cmH2O/L/s, but the actual Raw changes dynamically. Therefore, using Raw and Crs that are not precise to calculate MP that makes the calculation process of Eq. [2] more complicated, and the calculation result contains larger errors. It can be seen that the calculation result of Eq. [2] is smaller than that of Eq. [1], which may be that the actual Raw is smaller than the set value and/or the actual Crs is larger than the set value. In the original validation, over 50% of the ARDS patients were mild ARDS (PaO2/FiO2, 244±135 mmHg) and a short ICU stay (3.8±5.9 days). The application of MP in such patient group is less important compared to moderated and severe ARDS (7,17). But in this study, we simulated different ARDS lungs varied from mild to severe ARDS. The computed results varied depending on PEEP levels, which may also be explained by non-linear Crs within tidal breathing when recruitment and overdistension were presented in different PEEP levels. In actual operation, it is recommended to directly select Eq. [1] to calculate the MP during volume-controlled ventilation (VCV), which can effectively save calculation steps and reduce errors. Eq. [3] is a simplification of Eq. [1] and does not require to measure plateau pressure (Pplat). If the patient does not have a valid Plat measurement, MP can be calculated using this formula.
Pressure-controlled ventilation
During pressure-controlled ventilation (PCV), since the Paw dose not rise in a linear way, applying the formulas derived from VCV will cause obvious calculation errors. Hence, several formulas are proposed to calculate MP during PCV. Under the assumption of an ideal “square wave” Paw during inspiration, thus pressure rise time (Tslope) =0, the simplified formula, Eq. [6] is brought out. Eq. [5], proposed by van der Meijden et al., which is simpler than Becher’s approach and maybe match the physiology of PCV better (14,18). However, since , Eq. [5] can be roughly the same as Eq. [6]. However, in our study, during PCV, Tslopes varied from 0.63 to 1 s. The assumption that Tslope =0 would significantly ascend the value of MP. Therefore, MPs calculated with Eqs. [5] and [6] introduced significant biases. According to Becher et al. (10), Eq. [4] would be the most suitable one when the inspiratory pressure rise time is unneglectable, which is the case in the present study. Taken together, based on our study, we recommend using Eq. [4] for the calculation of MP during PCV.
Respiratory system compliance, PEEP, and RR
We also found that the change of Crs will influence the accuracy of the algebraic formulas under VCV (Table S1). As we kept Crs below LIP and beyond UIP constant, increasing Crs between LIP and UIP will increase the error using single Crs to represent the whole breath (18). Moreover, when changing Crs, it is actually simulating different degrees of ARDS. The lower the Crs is, the higher the degree of ARDS. When reviewing our research data, it can be found that the lower the Crs during VCV or PCV, the MPs calculated by equations are higher than the gold standard. When Crs ≥25 mL/cmH2O, the MPs calculated by equations are close to the gold standard (Table S1 and Table S3). Although the dominant method for grouping ARDS is based on the oxygenation index, we have also found a method, the Murray Lung Injury Score, that based on Crs, alveolar consolidation, hypoxemia, and PEEP (19). According to this Score, Crs bellowing 39 mL/cmH2O should be severe lung injury, which means in our study, most of our settings, setting Crs at 30 mL/cmH2O, should be simulating severe ARDS. Exceptions occur in Scenario 1, that we have settings of Crs =40 mL/cmH2O and Crs =45 mL/cmH2O, which maybe represent mild to moderate ARDS, and the calculating results of equations for these models are very similar to gold standard. However, we have also simulated the Crs from 10 to 20 mL/cmH2O, these models may represent very severe ARDS. On these cases, the calculating results of equations are larger than that of gold standard. Changing PEEP may influence the recruitment and overdistension, which again influence the volume-dependent Crs (20). The dominate factor for the errors with Eqs. [5] and [6] was mainly the Tslope, therefore, the change of PEEP or RR did not influence the error in MP calculation.
Limitations
Several limitations of the study have to be acknowledged. This is a simulation study with a lung simulator, TestChest. The advantage was that the lung mechanics were adjustable. Unfortunately, the lung physiology could not be 100% simulated. According to the manufacturer, the design of TestChest is based on our known lung physiological parameters and respiratory mechanics equations, but is far less complex than real human lungs. The compliance, SPO2 and FRC of TestChest can be changed automatically with clinical treatment changes, but other parameters are set fixed values, and the real human lung is that all physiological parameters can be changed with clinical treatment. Another example is respiratory system resistance. TestChest simulates a total resistance, while real human lung resistance is divided into elastic resistance and static resistance. In clinical treatment, there are more factors that affect the resistance due to the connection of the ventilator. Although the TestChest is the most intelligent and advanced lung simulator, all parameters are realized through the cooperation of various sensors, but there are still many gaps compared with the real human lung. As we simulate ARDS lungs, compared with the human lung, the lung’s “Heterogeneity” is difficult to achieve on the TestChest. Therefore, the response to ventilator settings may not represent the response of real patients. Furthermore, only a few data points were collected in each scenario and therefore, the statistical analysis might be underpowered.
Clinical practice
As we have discussed above, algebraic formulas may introduce bias during different circumstances. However, we think that in clinical practice, the most important thing for the MP is not only the “true” value but the trend. As we have observed and previous literature has reported, the trend of MP, calculated by the same algebraic formula for the same patient, is relatively credible. We use this trend to predict VILI and find it rather practical (21,22). Moreover, surrogate formulas are easier to be undertaken. According to the literature, ARDS patients with an MP more than 18 J/min would have higher mortality (17), and moderate and severe ARDS patients would have an increased risk of mortality with higher MP (23). In our daily practice, we usually use Eq. [3] as we have mentioned above. We start prone position ventilation in those patients with an MP over 17 J/min. If 2 to 3 J/min of the decrease cannot be achieved, we will start venous-venous extracorporeal membrane oxygenation (ECMO), often combining prone position ventilation. In the future, on the one hand, more clinical practice should be introduced to improve MP calculation by formulas. On the other hand, with the increasing computing power of ventilators, geometric methods should be integrated into ventilators to achieve more precise MP calculation.
Conclusions
The algebraic formulas may introduce considerably large bias under the presented lung conditions, especially in moderate to severe ARDS. Cautious is required when selecting adequate algebraic formulas to calculate MP based on the formula’s premises, ventilation mode, and patients’ status. In clinical practice, the trend rather than the value of MP calculated by formulas should require more attention.
Acknowledgments
Funding: This study was funded by the National Natural Science Foundation of China (No. 82270081) the National Key R&D Program of China (Nos. 2022YFC0869400 and 2022YFC2504402), the Emergency Key Program of Guangzhou Laboratory (Nos. SRPG23-001 and EKPG21-17) and the Natural Science Foundation of Guangdong Province, China (No. 2020A1515011459).
Footnote
Reporting Checklist: The authors have completed the STROBE reporting checklist. Available at https://jtd.amegroups.com/article/view/10.21037/jtd-22-1409/rc
Data Sharing Statement: Available at https://jtd.amegroups.com/article/view/10.21037/jtd-22-1409/dss
Conflicts of Interest: All authors have completed the ICMJE uniform disclosure form (available at https://jtd.amegroups.com/article/view/10.21037/jtd-22-1409/coif). The authors have no conflicts of interest to declare.
Ethical Statement: The authors are accountable for all aspects of the work in ensuring that questions related to the accuracy or integrity of any part of the work are appropriately investigated and resolved.
Open Access Statement: This is an Open Access article distributed in accordance with the Creative Commons Attribution-NonCommercial-NoDerivs 4.0 International License (CC BY-NC-ND 4.0), which permits the non-commercial replication and distribution of the article with the strict proviso that no changes or edits are made and the original work is properly cited (including links to both the formal publication through the relevant DOI and the license). See: https://creativecommons.org/licenses/by-nc-nd/4.0/.
References
- Bellani G, Laffey JG, Pham T, et al. Epidemiology, Patterns of Care, and Mortality for Patients With Acute Respiratory Distress Syndrome in Intensive Care Units in 50 Countries. JAMA 2016;315:788-800. [Crossref] [PubMed]
- Fan E, Brodie D, Slutsky AS. Acute Respiratory Distress Syndrome: Advances in Diagnosis and Treatment. JAMA 2018;319:698-710. [Crossref] [PubMed]
- Slutsky AS, Ranieri VM. Ventilator-induced lung injury. N Engl J Med 2013;369:2126-36. [Crossref] [PubMed]
- Marini JJ, Rocco PRM, Gattinoni L. Static and Dynamic Contributors to Ventilator-induced Lung Injury in Clinical Practice. Pressure, Energy, and Power. Am J Respir Crit Care Med 2020;201:767-74. [Crossref] [PubMed]
- Goligher EC, Ferguson ND, Brochard LJ. Clinical challenges in mechanical ventilation. Lancet 2016;387:1856-66. [Crossref] [PubMed]
- Costa ELV, Slutsky AS, Brochard LJ, et al. Ventilatory Variables and Mechanical Power in Patients with Acute Respiratory Distress Syndrome. Am J Respir Crit Care Med 2021;204:303-11. [Crossref] [PubMed]
- Gattinoni L, Tonetti T, Cressoni M, et al. Ventilator-related causes of lung injury: the mechanical power. Intensive Care Med 2016;42:1567-75. [Crossref] [PubMed]
- Silva PL, Ball L, Rocco PRM, et al. Power to mechanical power to minimize ventilator-induced lung injury? Intensive Care Med Exp 2019;7:38. [Crossref] [PubMed]
- Coppola S, Caccioppola A, Froio S, et al. Effect of mechanical power on intensive care mortality in ARDS patients. Crit Care 2020;24:246. [Crossref] [PubMed]
- Becher T, van der Staay M, Schädler D, et al. Calculation of mechanical power for pressure-controlled ventilation. Intensive Care Med 2019;45:1321-3. [Crossref] [PubMed]
- Giosa L, Busana M, Pasticci I, et al. Mechanical power at a glance: a simple surrogate for volume-controlled ventilation. Intensive Care Med Exp 2019;7:61. [Crossref] [PubMed]
- Zhao Z, Guttmann J, Möller K. Assessment of a volume-dependent dynamic respiratory system compliance in ALI/ARDS by pooling breathing cycles. Physiol Meas 2012;33:N61-7.
- organis-gmbh.ch. Organis. Available online: https://www.organis-gmbh.ch/solutions/testchest/. Accessed 30 May 2021.
- van der Meijden S, Molenaar M, Somhorst P, et al. Calculating mechanical power for pressure-controlled ventilation. Intensive Care Med 2019;45:1495-7. [Crossref] [PubMed]
- Zhao Z, Frerichs I, He H, et al. The calculation of mechanical power is not suitable for intra-patient monitoring under pressure-controlled ventilation. Intensive Care Med 2019;45:749-50. [Crossref] [PubMed]
- Serpa Neto A, Deliberato RO, Johnson AEW, et al. Mechanical power of ventilation is associated with mortality in critically ill patients: an analysis of patients in two observational cohorts. Intensive Care Med 2018;44:1914-22. [Crossref] [PubMed]
- Chiumello D, Gotti M, Guanziroli M, et al. Bedside calculation of mechanical power during volume- and pressure-controlled mechanical ventilation. Crit Care 2020;24:417. [Crossref] [PubMed]
- Guttmann J, Eberhard L, Fabry B, et al. Determination of volume-dependent respiratory system mechanics in mechanically ventilated patients using the new SLICE method. Technol Health Care 1994;2:175-91. [Crossref] [PubMed]
- Raghavendran K, Napolitano LM. Definition of ALI/ARDS. Crit Care Clin 2011;27:429-37. [Crossref] [PubMed]
- Maia LA, Samary CS, Oliveira MV, et al. Impact of Different Ventilation Strategies on Driving Pressure, Mechanical Power, and Biological Markers During Open Abdominal Surgery in Rats. Anesth Analg 2017;125:1364-74. [Crossref] [PubMed]
- Dianti J, Matelski J, Tisminetzky M, et al. Comparing the Effects of Tidal Volume, Driving Pressure, and Mechanical Power on Mortality in Trials of Lung-Protective Mechanical Ventilation. Respir Care 2021;66:221-7. [Crossref] [PubMed]
- Russotto V, Bellani G, Foti G. Respiratory mechanics in patients with acute respiratory distress syndrome. Ann Transl Med 2018;6:382. [Crossref] [PubMed]
- Zhang Z, Zheng B, Liu N, et al. Mechanical power normalized to predicted body weight as a predictor of mortality in patients with acute respiratory distress syndrome. Intensive Care Med 2019;45:856-64. [Crossref] [PubMed]


