
Multi-source dynamic ensemble prediction of infectious disease and application in COVID-19 case
Highlight box
Key findings
• Multi-source dynamic ensemble prediction model is proposed to reflect the multi-wave development trend and improve the accuracy of prediction. Based on the results, the accuracy rate has been improved significantly, which can reach to 88.94%.
What is known and what is new?
• Classic epidemic models, such as the susceptible-infected-removed (SIR) and the susceptible-exposed-infected-removed (SEIR) have been applied for predicting COVID-19. However, the prediction accuracy was not satisfying. It is of great importance to propose a new method to remedy the flaw.
• In this manuscript a new method called multi-dynamic ensemble prediction model, which incorporates a modified SEIR model to improve the accuracy of the prediction result.
What is the implication, and what should change now?
• MDEP method can depict the multiwave development of COVID-19. The MDEP method improved the prediction accuracy of COVID-19. With further application to other infectious diseases, the MDEP method will provide accurate predictions of infectious diseases and aid governments make appropriate directives.
Introduction
Three months after the discovery of coronavirus disease 2019 (COVID-19), the World Health Organization declared COVID-19 as a pandemic on 12 March, 2020 (1). To date, more than 190 countries and regions have reported COVID-19 cases, more than 527,000,000 people have been infected, and 6,000,000 people have died globally. The most recent global outbreak of COVID-19 has been triggered by the Omicron variant. The Omicron variant showed a higher transmissibility than the Delta variant (2), and the identification of its sub-lineages, namely BA.2.12.1, BA.4, and BA.5, even exhibited higher transmissibility than the original Omicron variant (3). Many countries have experienced a sharp increase in the number of confirmed cases of COVID-19, which has increased by 71% from 27 December, 2021 to 2 June, 2022 (4). Some researchers pointed out that current vaccines, such as ChAdOx1 nCoV-19 and BNT162b2, can only provide limited protection against Omicron variant (5), and according to a recent study, the Omicron wave will not end by November 2023 (6). How to make an early warning on the spread of COVID-19 and mitigate it have become a tricky question for governments. Except for the medical help, establishing a prediction system is also of great need.
The subject of infectious diseases has developed into an interdisciplinary field (7), which requires not only knowledge of the pathogen but also knowledge of statistics and mathematics (8). Mathematical models have been developed for predicting the development of infectious diseases in the epidemiology field (9). There are numerous studies have been conducted on making reliable prediction results on the development of COVID-19. For example, the clustering technique used in machine learning model has been implemented for forecasting the COVID-19 outbreak in Chinese provinces, and achieved stable results 2 days ahead of the present time (10). Apart from machine learning models, the classic epidemiological models, such as the susceptible-infected-removed (SIR) and susceptible-exposed-infected-removed (SEIR) models, can also depict the development of infectious diseases. However, such models can only predict one wave of an epidemic (11), while the real situation is most likely a multiwave epidemic. Multi-source infection is one of the reasons for the multiple waves of an epidemic. Particularly in highly urbanized areas, interaction between people is tight and frequent. When the detection speed is not as fast as the spread speed of the virus, potential patients cannot be diagnosed and hospitalized in time, and they will become a new source of infection and cause a new wave of the epidemic. This phenomenon has appeared several times in recent outbreaks of COVID-19 in China.
Since the first COVID-19 outbreak in China, the government has taken strict measures to contain the epidemic. The core principle of the Chinese government to contain the COVID-19 epidemic is to implement fast and strict non-pharmaceutical interventions (NPIs) to cut off the transmission chain (12). The quarantine, social distancing, and isolating infected people have been proved to be able to contain the epidemic in China (13). In addition, the most important thing is to ensure the capacity of healthcare will not be overloaded during the outbreak of COVID-19. Since the healthcare resources in communities that are distanced from major urban areas are limited (14), thus, these NPIs, including social distancing, testing, contact-tracing and quarantine, can relieve the healthcare burden and enable the reopening of economics (15). In fact, not only the COVID-19 epidemic can be curbed by applying NPIs, but also the SARS outbreak happened in 2022 can be controlled by isolating the infected individuals from susceptible population (16). Even though these NPIs worked well on small-scale domestic outbreaks of COVID-19 in China from April 2020 to December 2021, the large-scale human mobility has made it much easier for viruses to be transmitted among humans (17), particularly when people tend to take public transportation in cities, and this will increase the risk of infection by virus (18,19). The delayed detection of infected cases outside the lockdown areas would cause several sources of the epidemic, making it difficult for governments to control the development of COVID-19 in time. Considering this situation, a new method for predicting the multiwave spread of COVID-19 in megacities is required.
Epidemic models have long been used for predicting the development of infectious diseases. In this study, we applied a modified SEIR model and combined it with a multi-source dynamic ensemble prediction (MDEP) technique to predict the development of the latest COVID-19 epidemics in Beijing, Lanzhou, Beihai, Urumqi, Yili, and Sanya, China. We chose these cities as the target cities is because the spread patterns of COVID-19 are complex. Thus, the advantage of the implementation of the MDEP method can be clearly observed, and this method would provide a new perspective for predicting the spread of infectious diseases in populated areas. We present this article in accordance with the TRIPOD reporting checklist (available at https://jtd.amegroups.com/article/view/10.21037/jtd-23-234/rc).
Methods
Data sources
All the epidemic data of COVID-19 are available online and can be obtained publicly. Daily epidemic data for COVID-19 in Beijing city were obtained from the National Health Commission of the People’s Republic of China (http://www.nhc.gov.cn/xcs/yqtb/list_gzbd.shtml). The time period for COVID-19 data in Beijing was from 17 April 2022 to 8 June 2022. The epidemic data of COVID-19 in Lanzhou City were collected from the Health Commission of Gansu Province (http://wsjk.gansu.gov.cn/wsjk/c113605/list.shtml), and the time period was from 8 July 2022 to 9 August 2022. The COVID-19 epidemic data of Beihai City were collected from the Health Commission of Guangxi Zhuang Autonomous Region (http://wsjkw.gxzf.gov.cn/ztq_49630/sszt/xxgzbdfyyqfk/yqtb/) from 12 July 2022 to 12 August 2022. The COVID-19 data of Urumqi and Yili can be obtained from the Health Commission of Xinjiang Uygur Autonomous Region (http://wjw.xinjiang.gov.cn/hfpc/fkxxfyfkxx/fkxxfy_list.shtml) from 30 July 2022 to 20 September 2022. The COVID-19 data of Sanya city were downloaded from the Health Commission of Hainan Province (https://wst.hainan.gov.cn/swjw/rdzt/yqfk/index_5.html) from 1 August 2022 to 14 September 2022. All epidemiological data were collected and updated in a daily basis.
Modified SEIR model
The global prediction system of COVID-19 pandemic (GPCP) was used to predict the development of the COVID-19 outbreak in China. The GPCP system is the modified SEIR model. Compared to the classical epidemiological models, such as the SIR model and SEIR model, the modified SEIR model, also called the SPEIQDR model, adds three more stages, namely the protected stage (P), quarantined stage (Q), and dead stage (D) (20). Similar to the SIR and SEIR models, the modified SEIR model is a compartment model that depicts the population flow between each compartment. The modified SEIR model follows the following equations:
where the total population N=S+P+E+I+Q+D+R. The susceptible people will either enter the protected stage under the protection rate α, or become exposed people with the rate β, and the exposed people will take time, also known as latent time to become infectious, and there will be a certain part of the infected people being admitted to the hospital and become quarantined under the rate δ. The rates λ and κ represent the recovery and death rates, respectively, which suggests that quarantined people will recover or die after treatment. Particularly, the protection rate (α) represents the proportion of susceptible people who will be highly immune to COVID-19 due to the good awareness of self-protection, such as wearing face masks and keeping social distance. It should be noted that all the above-mentioned parameters are greater than zero, except the protection rate. When α>0, people will enter into protected phase from susceptible population, while if α<0, people will return to susceptible group (21). The initial value and range of each parameter in the model are shown in the Table 1.
Table 1
| Parameters | Range | Initial values |
|---|---|---|
| α (protection rate) | −1 to 1 | 0.06 |
| β (transmission rate) | 0 to 5 | 1.0 |
| γ (inverse of latent time) | 0 to 1 | 0.2 |
| δ (transition rate of infected people get quarantined) | 0 to 1 | 0.1 |
| λ (recovery rate) | 0 to 1 | 0.1 |
| κ (death rate) | 0 to 1 | 0.001 |
The GPCP system also sets up a parameterization scheme for atmospheric factors, including temperature and humidity. The original transmission rate β was calibrated as β=β0+β1F(T2m)+β2F(RH2m), where F(T2m) and F(RH2m) represent the probability distribution functions of temperature and humidity obtained by Huang et al. (22). T2m and H2m represents the temperature at 2 m above ground level and the humidity at 2 m above the ground level, respectively. β0 represents the original transmission rate when temperature and humidity are excluded, and β1 and β2 represent the transmission rates when temperature and humidity factors are included, respectively.
Model coefficients
Due to the difficulty of obtaining the coefficients needed in the model, we, therefore, adopted a method called inverting coefficients method to improve the goodness of fit of the model (23). Generally speaking, the initial values of each coefficient need to be provided to the model before making any predictions. After that, some optimization algorithms will be applied, and the real time epidemic data are used to invert the coefficients in the model, that is to say the parameters and real epidemical data are adjusted along the process of iteration. Therefore, the initial values of coefficients will be adjusted and updated to the real value, and the final coefficients will be substituted in the model to produce more accurate prediction results. However, it should be noted that the model is sensitive to the initial values, so it is essential to change the initial values enough times to achieve a robust result.
Parameters for control measurements
In the GPCP system, different parameterization schemes are employed into the model. As for MDEP method, the most important one is the parameterization for control measurements. Since Chinese government applied strict control measures in terms of contain the outbreaks in a timely manner. Therefore, to achieve a better performance of the prediction results, we established a parameterization scheme to depict the different effects of different strengths of control measures. There are three coefficients are included in the model, namely government response time (Days_con), initial exposed cases (E0), and the attenuation rate. In this case, the infection rate β will be calibrated as β=β0×attenuation ratet(t>Days_con), where β0 is the base infection rate. With the strict control measures applied, the value of Days_con will be smaller, and attenuation rate will be smaller. As a result, the duration of an outbreak will be shorter and the peak value and cumulative cases will be smaller.
As for the model for predicting the COVID-19 outbreaks in China, the same methodology was used. Moreover, to ensure that robustness of the prediction results, the Levenberg-Marquardt algorithm was introduced into the model (24,25). To be more specific, a damping coefficient is inserted into the Gauss-Newton method to calculate the Hessian matrix, which can converge much faster than before, and yield more robust results (26).
MDEP method
The forecasting problem is to predict the output information of the system in the future using the known current and past measurable information. It is not difficult to predict a deterministic dynamic system that does not consider the uncertain random factors of the system or its environment. However, random factors or multiple sources make forecasting difficult. For several practical epidemic transmission systems, the system model parameters are difficult to determine precisely in advance, or they change with the environment and its disturbance. The discovery of a new infection source can change the development of an epidemic, and the initial values of the parameters cannot satisfy the current situation. Therefore, it is necessary to construct a multisource dynamic ensemble prediction method to adjust the system model parameters to reduce the error rate of the model.
MDEP is a method that sums the initial prediction result and follow-up dynamic prediction results together to obtain the integrated result as the final prediction result. This is similar to the ensemble forecast that has been used in weather forecast since the 1990s (27). The integrated result is the sum of multiple ensemble predictions under different initial conditions. The aim of the MDEP method is to reduce the initial error caused by incomplete information provided by the initial data set (28). At the beginning of the prediction, we could only obtain limited information from the initial dataset. In some cases, when the epidemic has only one source of infection, the initial prediction has good accuracy. However, real situations are complex. For epidemics occurring in some cities, multiple sources of infection always emerge one after another. In this study, multisource refers to COVID-19 cases identified in non-lockdown or non-quarantined areas. The appearance of each infection source will likely cause a new wave of the epidemic, and the initial prediction cannot depict the multiwave epidemic. Therefore, the MDEP method has been proposed to solve this problem.
The integrated results are a set of data expressed as yi,j, where i represents the multi-source of the epidemic; for example, the result from the initial prediction stage was expressed as y0,j, and for the first dynamic prediction period, the result would be y1,j, and j represents the daily predicted results. In the initial prediction procedure, we obtained a set of prediction results: y0,1, y0,2, …, y0,n. With the development of the epidemic, multiple waves will occur, and we will use the MDEP method to obtain a set of new prediction results. For example, the prediction results for the first wave would be y1,5, y1,6, y1,7, …, y1,n, and the new prediction results would be superimposed on the previous ones; thus, the final prediction results of the epidemic should be y0,1, y0,2, y0,3, y0,4, y0,5+y1,5, y0,6+y1,6, y0,7+y1,7, …, y0,n+y1,n. As shown in Figure 1, the final prediction result is called the integrated result, and it will be updated i times, where i equals the number of waves the epidemic had and n equals the number of days that the epidemic lasts.
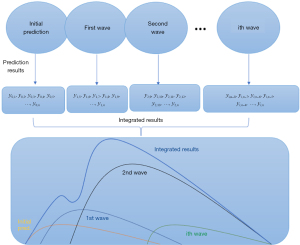
Results
The defect of the one-wave models
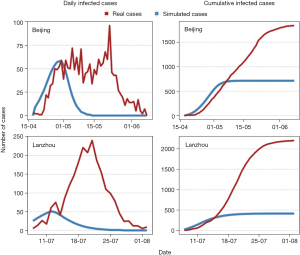
According to the nature of the classic SEIR and SIR models, only one wave of an epidemic can be simulated by these models. As shown in Figure 2, we take the recent outbreaks of COVID-19 in Beijing and Lanzhou cities as examples, where the red lines show the real development trends of COVID-19 epidemics in these two cities, and blue lines are the simulated results produced by the one-wave modified SEIR model. It can be observed clearly from Figure 2 that the real development trends of COVID-19 exhibit multiple waves, and fluctuate frequently at large scales. The simulated curves cannot reflect the real trends, and show very poor accuracy rates in daily cases and cumulative cases. The calculated error values (E=Npdaily/pcumu_i−Nrdaily/rcumu_i, where i=1,2,3… and Npdaily/pcumu_i represents the prediction results of daily and cumulative cases, while Npdaily/rcumu_i represents the real daily and cumulative cases), which are shown in Figure 3, indicated that the error values of daily and cumulative cases in Beijing and Lanzhou fluctuated greatly, ranging from −250 to 25 and −2,000 to 500, respectively. Since the classic epidemical models were proposed about 100 years ago, when implementing these models nowadays, they will of course have some defects. The most prominent flaw of these models is that they are compartment models, which means they are suitable for a limited and confined space, where the large-scale of human mobility will not be considered. Therefore, it cannot depict the real situation.

Multisource of infections
Except for the flaw of the models themselves, other factors also need to be emphasized. As the complex transmission pattern of COVID-19 epidemic in cities, such as frequent contact between people, there will be multi-source of infections identified during the outbreaks. In addition, the Omicron variant, which was identified in December 2021, possesses a higher transmissibility and is hard to be diagnosed in time, therefore, has contributed to the wide-scale outbreaks in China. Based on the previous experiences that the Chinese government has gained in terms of control the transmission of COVID-19, the most effective method is to isolate infected people. By using this method, the Chinese government has successfully contained previous outbreaks of COVID-19. However, as aforementioned, the complex transmission pattern of Omicron variant has caused multiple infection sources, and each of the new infection sources caused a new wave of the epidemic. The reason why the multi-sources of infection kept emerging is because of the appearance of the new cases in non-lockdown or non-quarantined areas. Figure 4 shows that when the number of cases outside the lockdown areas (red areas) increased, the total number of cases (blue areas) also increased. The development trend of the cases in non-lockdown or non-quarantined areas are accordance with it of the total number of cases, when the cases outside the lockdown or quarantined areas dropped to zero, the number of the total would decrease to zero in a few days.
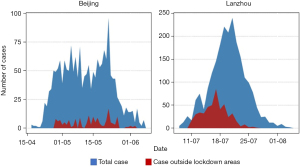
In order to remedy these defects, an innovative method named as MDEP method was proposed. The development of the case outside the lockdown areas was used as an important reference for dynamic prediction, that is, if the case outside the lockdown areas continues to emerge, the dynamic prediction must be carried out continuously.
Case study in China
Figure 4 shows the prediction results of MDEP for the recent COVID-19 outbreaks in Beijing, Lanzhou, Beihai, Urumqi, Yili, and Sanya cities. The prediction results are presented as daily confirmed cases and cumulative cases separately. From Figure 5, we can observe that the real epidemiological data fluctuated over a large scale, and clearly, the one-wave SEIR model could not depict the real trend. Therefore, we employed the MDEP prediction method to obtain more accurate results. The initial prediction on Beijing began on 22 April 2022 when the epidemic entered an outbreak phase, and ended on 4 May 2022. The number of daily confirmed cases on 4 May 2022 was 43, and the number of daily confirmed cases started increasing from 5 May 2022 to 9 May 2022 which implies that a new small resurge in the epidemic occurred. Because the initial prediction could not reflect the second increase phase, we performed the first dynamic prediction to update the original result. The duration of the first dynamic prediction was from 5 May 2022 to 10 May 2022. The second dynamic prediction started on 11 May 2022 and ended on 13 May 2022. The third dynamic prediction was from 14 May 2022 to 29 May 2022 which lasted for 16 days, and the fourth dynamic prediction started on 30 May 2022. We superimposed the initial prediction, first dynamic prediction, second dynamic prediction, third dynamic prediction, and fourth dynamic prediction to obtain the final result. As shown in Figure 5, the blue line represents the final result, which is labelled as the integrated prediction. From the plot, we observe that the MDEP method can reflect multiple waves of the epidemic, which is more suitable for real-world situations. The prediction results for the cumulative cases also suggest that the MDEP method can produce a more accurate result. Based on the predicted results, there will be 1,848 confirmed cases by the end of the outbreak. The real number of confirmed cases was 1,840 as of 8 June 2022 since there had been no new confirmed cases reported outside the lockdown areas, and the government declared that the outbreak of COVID-19 had been contained successfully.

After successfully implementing the MDEP method on COVID-19 outbreaks in Beijing, we then utilized this method on another five cities in China, namely Lanzhou, Beihai, Urumqi, Yili, and Sanya. These cities all shared the same features, which are the duration of the COVID-19 outbreaks were relative long, and the fluctuations of daily cases were large. Therefore, the development trends of COVID-19 epidemics in these cities are consistent with multiwave development of COVID-19. In addition, all the six cities were hit by Omicron variant, so the interference of different variants was excluded, thus, ensure the results are not biased. Lanzhou reported the first confirmed case of COVID-19 on 8 July 2022, and we applied the MDEP method to predict the spread of COVID-19 in Lanzhou. The results are shown in Figure 5. The prediction results for the cumulative cases showed a high accuracy. The COVID-19 outbreak in Lanzhou ended on 5 August 2022, with the real cumulative cases is 2,208, and final prediction results for cumulative cases is 2,234. Beihai is a tourist city located in Guangxi Province. The first confirmed case was reported on 12 July, 2022. Following the first confirmed case, the COVID-19 epidemic in Beihai exhibited a rapid growth trend, and it took a month for the government to control the development of the epidemic. The prediction results indicate that the initial prediction began on 12 July 2022 and ended on 17 July 2022 followed by the first dynamic prediction (from 18 July 2022 to 21 July 2022), and the second dynamic prediction (from 22 July 2022 to 12 August 2022). The outbreak of COVID-19 in Beihai ended on 12 August 2022 with a final cumulative number of cases of 3,202, and our prediction result was 3,220. The MDEP method showed a high accuracy in the final result. The same procedure was conducted on Urumqi, Yili, and Sanya cities, and the prediction results are shown in Figure 5. The final results suggested that by the time when COVID-19 outbreaks ended, there would be 1,073, 2,700, and 16,619 confirmed cases in Urumqi, Yili, and Sanya, respectively, while the real cases in these three cities were 1,172, 2,864, and 15,668, respectively. According to the prediction results, we can conclude that the MDEP method has shown a high accuracy in terms of predicting the multiwave of COVID-19. When taking the population and control measures into consideration, we can observe that cities like Beijing, Lanzhou and Urumqi took relatively strict control measures compared with the other three cities, and they all have shown lower peak values and shorter durations
Model validation
Figure 6 validates the prediction results. The validation results indicated that our predictions of cumulative cases exhibited high accuracy rates in Beijing, Lanzhou, Beihai, Urumqi, Yili, and Sanya. Figure 6A shows the scatter plot of predicted cases versus real confirmed cases. From the plot we can observe that the results show a strong goodness fit of the MDEP model. Moreover, the calculated R-square values shown in Table 2 prove that the MDEP model produced higher accuracy rates than the one-wave model did, as the R-square vales of MDEP model are very close to 1. The root mean square error (RMSE) values of the MDEP model in Beijing, Lanzhou, Beihai, Urumqi, Yili, and Sanya are 54.22, 47.25, 49.33, 71.49, 86.03, and 606.27, respectively, which are much smaller than it of the one-wave model, thus, illustrates that the MDEP model has a better performance in terms of predicting the development of COVID-19. The average accuracy rates are shown in Figure 6B, the accuracy rates of MDEP model (blue bar) of these six cities are all above 80%, with the accuracy rates are 89.95%, 91.74%, 94.81%, 81.08%, 85.50%, and 90.57% in Beijing, Lanzhou, Beihai, Urumqi, Yili, and Sanya, respectively, and the overall average accuracy rate is 88.94%. However, the accuracy rates of the one wave model (red bar) are much lower than MDEP model, with the overall average accuracy rate only 44.19%, which is the half of the accuracy rate of MDEP model. The differences of the accuracy rates are mainly caused by the different abilities in terms of management and healthcare of local governments. For example, Beijing possessed the developed healthcare system and has abundant resources to conduct contact tracing work, thus, even though there were many sources of infections, Beijing still managed to control the epidemic well. However, Urumqi and Yili have limited resources, and the outbreaks in these two cities were large, which exhausted the healthcare and management resources. Therefore, the transmission in these two cities showed the same characteristic, which is the ending periods, when the number of daily cases dropped below 10 and entering into the finishing phase, are longer than the rest of the cities. As a result, they had lower accuracy rates.
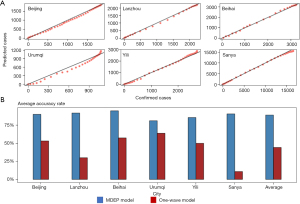
Table 2
| City statistic | Beijing | Lanzhou | Beihai | Urumqi | Yili | Sanya |
|---|---|---|---|---|---|---|
| R-square (one-wave model) | −0.33 | −0.72 | −0.24 | 0.05 | −0.19 | −0.33 |
| R-square (MDEP model) | 0.992 | 0.997 | 0.998 | 0.966 | 0.993 | 0.990 |
| RMSE (one-wave model) | 675.52 | 1,184.87 | 1,383.65 | 304.10 | 1,134.06 | 11,669.58 |
| RMSE (MDEP model) | 54.22 | 47.25 | 49.33 | 71.49 | 86.03 | 606.27 |
RMSE, root mean square error; MDEP, multi-source dynamic ensemble prediction.
Discussion
From the early stage of the COVID-19 pandemic, the Chinese government employed a zero-policy to contain the spread of COVID-19 (29). This policy has successfully stopped many domestic COVID-19 outbreaks. However, the recent situation has changed. The newly identified variant of coronavirus, known as the Omicron variant, has shown rapid transmissibility and triggered a huge outbreak worldwide. The Omicron variant first spread to mainland China on 8 January 2022 and the following domestic outbreaks of COVID-19 were all related to the Omicron variant. The recent outbreaks of COVID-19 in China showed some characteristics such as the long duration of the epidemic and the multiple sources of infections identified, which have not been discovered previously. These characteristics made the outbreaks difficult to contain in a timely manner and also added many difficulties to the prediction work.
In this study, we demonstrated the different characteristics of the COVID-19 outbreak in terms of the scale, duration, and infection sources. We observed that when the scale of the outbreak of COVID-19 was small, which indicated that the amplitude of the daily cases throughout the outbreak was small, this outbreak would possibly have a single infection source, and the source of the outbreak could be traced easily. Therefore, implementing effective measures to contain the outbreak is easier for governments. Outbreaks that satisfy the above-mentioned characteristics can be predicted using a one-wave modified SEIR model, and the results show relatively high accuracy rates. However, with the development of COVID-19, the mutated virus became harder to identify and had a higher transmissibility than the original one (30). Thus, the current situation has become more complicated. Particularly when large-scale human mobility makes the interaction between humans more frequent and provides a perfect opportunity for the transmission of the virus (31). Moreover, more frequent human mobility indicates more importation and exportation of humans, which will increase the risk of transmission of the virus (32). The MDEP method was proposed to solve this particular problem, and our prediction results have shown very high accuracy rates for the final confirmed cumulative cases. The average accuracy rates for daily cumulative cases were also high enough to be considered as good predictions.
Conclusions
Although the implementation of MDEP for COVID-19 is innovative and has been proven to be highly accurate. The limitations of this method cannot be ignored, because the base model used in the MDEP method is the modified SEIR model, which is a compartment model. The compartment model can reflect the internal transmission progress; in our case, it is the progress that people transferred from the susceptible stage either to the protected or exposed stages, and from the exposed to the infected stages, the infected people will be quarantined and finally recover or die. The major limitation of this compartment model is that the total population is assumed to be constant throughout the entire process, while in the real world, the total population always keeps changing, which indicates that external human mobility was not considered in the model. Some studies showed that take human mobility into consideration will improve the forecast accuracy (33), and quantifying the trade-off between mobility and infection can provide guidelines for governments to make appropriate directives (34). In addition, demographic data such as age, gender, and income were not considered in the model, as well as some digital data from social medium may provide earlier indication that help to make prediction in time (35). Moreover, the details of the epidemic data need to be improved. For instance, the reported date and illness onset date of the patients should be obtained and added into model to simulate the results accordingly, thus, compare the difference between these two simulation results to reveal more transmission mechanisms of COVID-19. In the next generation of our model, we will combine the MDEP model with an artificial intelligence model use more sources of data to make our model more suitable for complex conditions, such as large-scale human mobility and the transportation connection between cities, provinces, states, and countries. At the same time, we will also seek for cooperation and other ways to obtain more relevant data to perfect our model. However, the current MDEP model has significantly improved the prediction accuracy rate, and the prediction result can provide scientific guidance to the government and assist to make appropriate directives to cope with the domestic COVID-19 outbreak.
Acknowledgments
Funding: This work was jointly supported by the Self-supporting Program of Guangzhou Laboratory (No. SRPG22-007); The Collaborative Research Project of the National Natural Science Foundation of China (No. L2224041) and the Chinese Academy of Sciences (No. XK2022DXC005); Frontier of Interdisciplinary Research on Monitoring and Prediction of Pathogenic Microorganisms in the Atmosphere; and Gansu Province Intellectual Property Program (Oriented Organization) Project (No. 22ZSCQD02).
Footnote
Provenance and Peer Review: This article was commissioned by the Guest Editors (Jing Cheng, Tao Xu, Zifeng Yang, Wenda Guan) for the series “Current Status of Diagnosis and Forecast of COVID-19” published in Journal of Thoracic Disease. The article has undergone external peer review.
Reporting Checklist: The authors have completed the TRIPOD reporting checklist. Available at https://jtd.amegroups.com/article/view/10.21037/jtd-23-234/rc
Peer Review File: Available at https://jtd.amegroups.com/article/view/10.21037/jtd-23-234/prf
Conflicts of Interest: All authors have completed the ICMJE uniform disclosure form (available at https://jtd.amegroups.com/article/view/10.21037/jtd-23-234/coif). The series “Current Status of Diagnosis and Forecast of COVID-19” was commissioned by the editorial office without any funding or sponsorship. The authors have no other conflicts of interest to declare.
Ethical Statement: The authors are accountable for all aspects of the work in ensuring that questions related to the accuracy or integrity of any part of the work are appropriately investigated and resolved.
Open Access Statement: This is an Open Access article distributed in accordance with the Creative Commons Attribution-NonCommercial-NoDerivs 4.0 International License (CC BY-NC-ND 4.0), which permits the non-commercial replication and distribution of the article with the strict proviso that no changes or edits are made and the original work is properly cited (including links to both the formal publication through the relevant DOI and the license). See: https://creativecommons.org/licenses/by-nc-nd/4.0/.
References
- Ciotti M, Ciccozzi M, Terrinoni A, et al. The COVID-19 pandemic. Crit Rev Clin Lab Sci 2020;57:365-88. [Crossref] [PubMed]
- Saxena SK, Kumar S, Ansari S, et al. Characterization of the novel SARS-CoV-2 Omicron (B.1.1.529) variant of concern and its global perspective. J Med Virol 2022;94:1738-44. [Crossref] [PubMed]
- Cao Y, Yisimayi A, Jian F, et al. BA.2.12.1, BA.4 and BA.5 escape antibodies elicited by Omicron infection. Nature 2022;608:593-602. [Crossref] [PubMed]
- Taylor L. Covid-19: Omicron drives weekly record high in global infections. BMJ 2022;376:o66. [Crossref] [PubMed]
- Andrews N, Stowe J, Kirsebom F, et al. Covid-19 Vaccine Effectiveness against the Omicron (B.1.1.529) Variant. N Engl J Med 2022;386:1532-46. [Crossref] [PubMed]
- Zhao Y, Huang J, Zhang L, et al. Is the Omicron variant of SARS-CoV-2 coming to an end? Innovation (Camb) 2022;3:100240. [Crossref] [PubMed]
- Heesterbeek H, Anderson RM, Andreasen V, et al. Modeling infectious disease dynamics in the complex landscape of global health. Science 2015;347:aaa4339. [Crossref] [PubMed]
- Rock K, Brand S, Moir J, et al. Dynamics of infectious diseases. Rep Prog Phys 2014;77:026602. [Crossref] [PubMed]
- Gandon S, Day T, Metcalf CJE, et al. Forecasting Epidemiological and Evolutionary Dynamics of Infectious Diseases. Trends Ecol Evol 2016;31:776-88. [Crossref] [PubMed]
- Liu D, Clemente L, Poirier C, et al. Real-Time Forecasting of the COVID-19 Outbreak in Chinese Provinces: Machine Learning Approach Using Novel Digital Data and Estimates From Mechanistic Models. J Med Internet Res 2020;22:e20285. [Crossref] [PubMed]
- Singh P, Gupta A. Generalized SIR (GSIR) epidemic model: An improved framework for the predictive monitoring of COVID-19 pandemic. ISA Trans 2022;124:31-40. [Crossref] [PubMed]
- Zhang S, Wang Z, Chang R, et al. COVID-19 containment: China provides important lessons for global response. Front Med 2020;14:215-9. [Crossref] [PubMed]
- Anderson RM, Heesterbeek H, Klinkenberg D, et al. How will country-based mitigation measures influence the course of the COVID-19 epidemic? Lancet 2020;395:931-4. [Crossref] [PubMed]
- Miller IF, Becker AD, Grenfell BT, et al. Disease and healthcare burden of COVID-19 in the United States. Nat Med 2020;26:1212-7. [Crossref] [PubMed]
- Aleta A, Martín-Corral D, Pastore Y, Piontti A, et al. Modelling the impact of testing, contact tracing and household quarantine on second waves of COVID-19. Nat Hum Behav 2020;4:964-71. [Crossref] [PubMed]
- Gumel AB, Ruan S, Day T, et al. Modelling strategies for controlling SARS outbreaks. Proc Biol Sci 2004;271:2223-32. [Crossref] [PubMed]
- López L, Rodó X. The end of social confinement and COVID-19 re-emergence risk. Nat Hum Behav 2020;4:746-55. [Crossref] [PubMed]
- Chinazzi M, Davis JT, Ajelli M, et al. The effect of travel restrictions on the spread of the 2019 novel coronavirus (COVID-19) outbreak. Science 2020;368:395-400. [Crossref] [PubMed]
- Zhu R, Anselin L, Batty M, et al. The effects of different travel modes and travel destinations on COVID-19 transmission in global cities. Sci Bull (Beijing) 2022;67:588-92. [Crossref] [PubMed]
- López L, Rodó X. A modified SEIR model to predict the COVID-19 outbreak in Spain and Italy: Simulating control scenarios and multi-scale epidemics. Results Phys 2021;21:103746. [Crossref] [PubMed]
- Liu X, Huang J, Li C, et al. The role of seasonality in the spread of COVID-19 pandemic. Environ Res 2021;195:110874. [Crossref] [PubMed]
- Huang J, Zhang L, Liu X, et al. Global prediction system for COVID-19 pandemic. Sci Bull (Beijing) 2020;65:1884-7. [Crossref] [PubMed]
- Huang J, Yi Y, Wang S, et al. An analogue-dynamical long-range numerical weather prediction system incorporating historical evolution. Q J R Meteorol Soc 1993;119:547-65. [Crossref]
- Madsen K, Nielsen HB, Tingleff O. Methods for non-linear least squares problems. (2nd ed.) Society for Industrial & Applied Mathematics; 2004.
- Zhang L, Huang J, Yu H, et al. Optimal parameterization of COVID-19 epidemic models. Atmospheric and Oceanic Science Letters 2021;14:100024. [Crossref]
- Kőházi-Kis A. Relative effectiveness of the trust-region algorithm with precise second order derivatives. GRADUS 2019;6:1-7.
- Zhu Y. Ensemble forecast: A new approach to uncertainty and predictability. Adv Atmos Sci 2005;22:781-8. [Crossref]
- Palmer TN, Molteni F, Mureau R, et al. Ensemble prediction. InProc. ECMWF Seminar on Validation of models over Europe. Reading, United Kingdom: European Centre for Medium-Range Weather Forecasts; 1993;1:21-66.
- Huang L. Adjusted control rate closely associated with the epidemiologic evolution of the recent COVID-19 wave in Shanghai, with 94.3% of all new cases being asymptomatic on first diagnosis. J Infect 2022;85:e89-91. [Crossref] [PubMed]
- Greaney AJ, Loes AN, Crawford KHD, et al. Comprehensive mapping of mutations in the SARS-CoV-2 receptor-binding domain that affect recognition by polyclonal human plasma antibodies. Cell Host Microbe 2021;29:463-476.e6. [Crossref] [PubMed]
- Zhang M, Wang S, Hu T, et al. Human mobility and covid-19 transmission: A systematic review and Future Directions. Ann GIS 2022;28:501-14. [Crossref]
- Nakamura H, Managi S. Airport risk of importation and exportation of the COVID-19 pandemic. Transp Policy (Oxf) 2020;96:40-7. [Crossref] [PubMed]
- Schoot Uiterkamp MHH, Gösgens M, Heesterbeek H, et al. The role of inter-regional mobility in forecasting SARS-CoV-2 transmission. J R Soc Interface 2022;19:20220486. [Crossref] [PubMed]
- Gösgens M, Hendriks T, Boon M, et al. Trade-offs between mobility restrictions and transmission of SARS-CoV-2. J R Soc Interface 2021;18:20200936. [Crossref] [PubMed]
- Kogan NE, Clemente L, Liautaud P, et al. An early warning approach to monitor COVID-19 activity with multiple digital traces in near real time. Sci Adv 2021;7:eabd6989. [Crossref] [PubMed]


