Misuse of statistics in surgical literature

Introduction

Research in surgical literature is essential for furthering knowledge, understanding new clinical questions, as well as improving surgical technique yet surgical research provides unique methodology challenges compared to nonsurgical clinical studies (1). Biostatistics provides clinicians and researchers with the tools necessary to analyze associations and relationships within the data. The type of statistical analysis used, and consequently the data results depend on many factors: appropriate study design, type of data, proper selection and application of statistical methods, distribution of the data, and correct interpretations of the results (2,3). Statistics are therefore used to evaluate relationships and trends in data results. Published literature and data help clinicians and researchers deal with the increasing complexity and advancements in medical care such as new treatments, regulations, policies and public safety concerns (4).

Surgical education peer-reviewed publications have markedly increased over the last decade (5). The statistical complexity of the research in clinical surgery is also increasing (4). Literature in the 1970s showed that t-tests (approximately 44% in one study) (6) and descriptive statistics (i.e., means, standard deviations, range, etc.) were the most commonly used statistical tests of the time (6,7). Statistical methods have since become more complex with a variety of tests and sub-analyses that can be used to interpret, understand and analyze data. However, while the complexity of statistical analysis and the tools at researchers’ disposal have increased, basic statistical tests, such as the t-test, continue to be used as a primary statistical test in surgical research (8). Oftentimes incorrect tests are carried out despite the type of study and/or data. Recent reviews of published peer-reviewed literature concluded that nearly 50% of the clinical research publications contain at least one statistical error, some of which may have meaningful impacts on the results and interpretation (9-11).

In an Australia analysis of surgical literature, 71 out of 91 analytical papers (78%) contained errors in the usage of non-descriptive statistics. The papers often failed to test for significance when appropriate, quoted probability values without reference to the specific test used, and misused basic statistical techniques (12). Another study assessed 100 orthopedic surgery papers using a validated questionnaire. This study found 17% of the study conclusions were not justified by the results, and in 39% of the studies a different analysis should have been undertaken (13).

Overall, statistical analysis plays a large role in clinicians’ and researchers’ ability to understand associations and relationships between variables within the data. Although statistical models have become more complex in recent years, basic parametric statistical tests continue to be used at a high rate (14).

This paper aims to describe and evaluate the use and misuse of statistical methods and analyses in surgical literature. We will also provide information on which tests are currently being used, which tests should be used depending on the data and study design, and finally information on how to perform and come up with an appropriate statistical analysis plan for future surgical research.

Choice of statistical test

Many factors dictate the type of statistical test used when analyzing research data: study design, research questions and the type of data (15). For example, the choice of statistical tests would differ whether a research study aims to evaluate for a statistical difference compared to statistical similarities between treatment options, potential surgical approaches or other forms of “exposures” (14). If the underlying research methods are not appropriately identified prior to creation of an analysis plan, significant mistakes and potential misinterpretation of results are more likely. The consequence of applying the wrong statistical test ranges from minor, such as a relative shortcoming in methods, to significant, such as nullifying research results and conclusions (16).

Broadly, statistical tests are divided into two groups- those that assess differences versus similarities in the data. The most common type of tests used in research evaluates if differences exists among the data (17). These tests include one sided and two sided tests. A one sided test determines if the statistical difference occurs in only one direction (only better, only higher, etc.), while a two sided test assesses if the different occurs in either direction (better or worse, higher or lower, etc.). One sided tests are less conservative than two sided tests. To achieve statistical significance with a 2 sided test means that a one sided test of the same type on the same data achieves statistical significance by definition.

The equivalence and non-inferiority tests (18,19) evaluate if data is similar. Equivalence and non-inferiority is not the same as stating that the data is not statistically different (19). Equivalence and non-inferiority tests are often used to evaluate new tools, surgical approaches or treatments (20). Equivalence tests demonstrate that the new surgical approach has the statistically same outcome as the current surgical approach, similar to a two sided test. Non-inferiority tests are more akin to a one sided test, where the statistical evaluation is to test if the new surgical approach is at least as good as the current surgical approach. The new test may be statistically better, but a non-inferiority test will not detect if it is better, only that it is as good as the current approach.

Data type (numeric or categorical) and distribution (normal or not normal) dictate the specific tests to use (17). Traditionally, surgical trials relied upon independent sample t-tests in a traditional experimental vs. control model, or a paired sample t-tests if the test compared the same patient before and after the intervention. However, this approach likely oversimplifies data analyses. Table 1 summarizes the appropriate options available for statistical analysis depending on the type of data comparison and outcome required (7,13,14,21-24).

Table 1 Statistical tests for assessing differences based on the type of comparison and type of outcome data
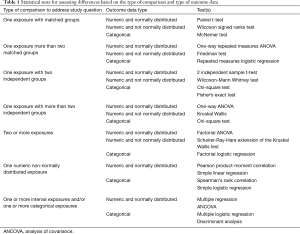
Full table

Oversimplification of analyses

Although the statistical complexity of research in clinical surgery is increasing (4), basic statistical tests and simple models continue to be used despite overall advancement in statistical analysis in research. A review of 240 surgical publications reported that basic parametric statistics were used in 60% of the publication, of those, 21% of publications failed to document a measure of central tendency and 10% did not state which type of evaluative statistic was used to calculate a P value (8). In order to use a parametric statistical test, such as a t-test, the data must be normally distributed. For many variables of interest, researchers do not know if the data are normally distributed or not. A common mistake in research assumes that all data are normal or follows the bell-shaped pattern (14) therefore leading to inappropriate statistical analysis.

Although complex statistical models are available to use, many datasets are not normally distributed yet basic parametric statistics continue to be used at a seemingly high rate (60%) within surgical literature (8). Instead, non-parametric tests are the appropriate choice for non-normally distributed data. For example, instead of relying on a t-test to test for differences between groups, researchers could use the Mann-Whitney U test for independent groups and the Sign test and Wilcoxon’s matched pairs test for dependent groups.

Exclusion of data

When and if to exclude data is a common question for all researchers. Exclusion of data should only be done in very limited situations, ideally ones that were considered prior to collecting data (12,25). Protocol failure, testing error, lab error, or equipment failure are unfortunately common in research (14). Situations that can potentially result in invalid data should be considered and accounted for prior to data collection. These events should be mitigated or removed through appropriate study protocols (e.g., equipment calibrated before every test). A plan to identify and handle data issues should be documented prior to collecting and analyzing the data. Reasons to exclude data should include a documented protocol deviation or lab error, not simply explained as outside of expected data outcomes (e.g., two standard deviations above the mean). A meta-analysis examined alteration and fabrication of research data and concluded that over a third (33.7%) of surveyed researchers admitted to “questionable” research methodologies (25) including: changing results to strengthen the finding; dubious data interpretation; suppression of methodological or critical details; exclusion of datum or multiple data due of a “gut feeling that they were inaccurate”; and misleading or selective reporting of study design, data or results.

Conclusions

With the growth of clinical research, data analyses have become increasingly complicated. Despite advancements in statistics, a large proportion of surgical research analysis has not adopted appropriate statistical testing methods as indicated for the type of data researched. Surgical research methodology can easily be approved by proper identification of the study design, study question and types of data to be analyzed. These simple steps are key to identify proper statistical analytical methods. Exclusion of data should be avoided unless absolutely indicated and appropriately documented. Proper consideration of these elements helps ensure appropriate analyses are conducted and valid data resulted.

Acknowledgements

Funding: This study has been funded, in part, by grants from the National Institute for Occupational Safety and Health (NIOSH/CDC) Education and Research Center training grant T42/CCT810426-10. The CDC/NIOSH is not involved in the study design, data analyses or interpretation of the data.

Footnote

Conflicts of Interest: The authors have no conflicts of interest to declare.

References

1. Demange MK, Fregni F. Limits to clinical trials in surgical areas. Clinics (Sao Paulo) 2011;66:159-61. [Crossref] [PubMed]
2. Thiese MS, Arnold ZC, Walker SD, et al. The misuse and abuse of statistics in biomedical research. Biochem Med (Zagreb) 2015;25:5-11. [Crossref] [PubMed]
3. Cassidy LD. Basic concepts of statistical analysis for surgical research. J Surg Res 2005;128:199-206. [Crossref] [PubMed]
4. Kurichi JE, Sonnad SS. Statistical methods in the surgical literature. J Am Coll Surg 2006;202:476-84. [Crossref] [PubMed]
5. Derossis AM, DaRosa DA, Dutta S, et al. A ten-year analysis of surgical education research. Am J Surg 2000;180:58-61. [Crossref] [PubMed]
6. Emerson JD, Colditz GA. Use of statistical analysis in the New England Journal of Medicine. N Engl J Med 1983;309:709-13. [Crossref] [PubMed]
7. Feinstein AR. Clinical biostatistics. XXV. A survey of the statistical procedures in general medical journals. Clin Pharmacol Ther 1974;15:97-107. [Crossref] [PubMed]
8. Oliver D, Hall JC. Usage of statistics in the surgical literature and the 'orphan P' phenomenon. Aust N Z J Surg 1989;59:449-51. [Crossref] [PubMed]
9. Gore SM, Jones IG, Rytter EC. Misuse of statistical methods: critical assessment of articles in BMJ from January to March 1976. Br Med J 1977;1:85-7. [Crossref] [PubMed]
10. Kim JS, Kim DK, Hong SJ. Assessment of errors and misused statistics in dental research. Int Dent J 2011;61:163-7. [Crossref] [PubMed]
11. White SJ. Statistical errors in papers in the British Journal of Psychiatry. Br J Psychiatry 1979;135:336-42. [Crossref] [PubMed]
12. Hall JC, Hill D, Watts JM. Misuse of statistical methods in the Australasian surgical literature. Aust N Z J Surg 1982;52:541-3. [Crossref] [PubMed]
13. Parsons NR, Price CL, Hiskens R, et al. An evaluation of the quality of statistical design and analysis of published medical research: results from a systematic survey of general orthopaedic journals. BMC Med Res Methodol 2012;12:60. [Crossref] [PubMed]
14. Greenland S, Senn SJ, Rothman KJ. at al. Statistical tests, P values, confidence intervals, and power: a guide to misinterpretations. Eur J Epidemiol 2016;31:337-50. [Crossref] [PubMed]
15. Hulley SB, Cummings SR, Browner WS, et al, editors. Designing Clinical Research. 4th ed. Lippincott Williams & Wilkins, 2013.
16. Jamart J. Statistical tests in medical research. Acta Oncol 1992;31:723-7. [Crossref] [PubMed]
17. Woolson RF, Clarke WR. editors. Statistical Methods for the Analysis of Biomedical Data. 2nd ed. New York, United States: John Wiley & Sons, 2000:Vol. 371.
18. Altman DG, Bland JM. Measurement in medicine: the analysis of method comparison studies. Statistician 1983;32:307-17. [Crossref]
19. Wellek S. editor. Testing Statistical Hypotheses of Equivalence and Noninferiority. 2nd ed. CRC Press, 2010.
20. D'Agostino RB Sr, Massaro JM, Sullivan LM. Non-inferiority trials: design concepts and issues - the encounters of academic consultants in statistics. Stat Med 2003;22:169-86. [Crossref] [PubMed]
21. Gore A, Kadam Y, Chavan P, et al. Application of biostatistics in research by teaching faculty and final-year postgraduate students in colleges of modern medicine: A cross-sectional study. Int J Appl Basic Med Res 2012;2:11-6. [Crossref] [PubMed]
22. Lang T, Secic M. How to Report Statistics in Medicine: Annotated Guidelines for Authors, Editors, and Reviewers, 2nd ed. Philadelphia: American College of Physicians, 2006.
23. Little RJ, Rubin DB. editors. Statistical Analysis with Missing Data. 2nd ed. John Wiley & Sons, 2014.
24. Hollander M, Wolfe DA, Chicken E. editors. Nonparametric statistical methods. 3rd ed. Hoboken, NJ: John Wiley & Sons, 2013.
25. Fanelli D. How many scientists fabricate and falsify research? A systematic review and meta-analysis of survey data. PLoS One 2009;4:e5738. [Crossref] [PubMed]