
Automatic 3D coronary artery segmentation based on local region active contour model
Highlight box
Key findings
• The combination of vesselness measure with a local region active contour model guided by vascular skeleton can significantly improve the segmentation effect of coronary arteries.
What is known and what is new?
• The local region active contour model can be used to segment coronary arteries.
• Before segmentation, the coronary skeleton was extracted and vesselness measure was added to the active contour model.
What is the implication, and what should change now?
• To achieve more effective segmentation of coronary arteries using active contour models in computed tomography angiography images, it is essential to consider more than just the intensity features of the image. Additional prior information, such as the precise position and local structure of the coronary arteries, is crucial for accurate segmentation.
Introduction
Cardiovascular disease has been the main cause of death in recent years (1), with the majority being caused by coronary artery disease (CAD). CAD is related to the accumulation of cholesterol and fat substances in the coronary arteries, which can lead to blockage of the vascular system supplying blood to the cardiac muscle system, resulting in heart disease, which can be fatal. Nowadays, cardiovascular disease is an increasingly prevalent disease in both developed and developing countries around the world. From a clinical perspective, coronary computed tomography angiography (CTA) utilizes injection of iodinated contrast agents to visualize the anatomical structure of coronary arteries. It is a widely used, non-invasive, and highly sensitive imaging method for routine clinical diagnosis of cardiovascular diseases. In clinical trials, coronary artery segmentation is an essential step in a series of tasks such as plaque assessment, stenosis detection, and centerline extraction (2). Describing the coronary artery in CTA images can help detect stenosis, obstruction, and other vascular abnormalities within the coronary artery, which is crucial for clinical decision-making such as drug selection and interventional treatment. Therefore, automatic coronary artery segmentation methods not only need to achieve high segmentation accuracy but also maximize the structural integrity of coronary artery formation. However, accurate segmentation of coronary arteries in CTA images is a challenging task due to factors such as significant noise, partial volume effects, and varying vessel sizes, especially uneven intensity distribution and branching heights. At present, the location and severity of narrowing plaques in CTA images need to be manually evaluated by radiologists. The precise segmentation of coronary arteries usually relies on the manual depiction of each CTA slice by radiologists, which is not only time-consuming but also prone to misdiagnosis and omission. Therefore, there is an urgent need for automatic segmentation of coronary arteries in CTA images to achieve an automatic and objective system for detecting coronary artery stenosis and plaques.
Vascular feature enhancement is usually performed prior to vessel segmentation. Vessels in medical images can usually be modeled as tubular structures whose cross sections can be described as asymmetric circles or ellipses (3). Based on this geometric structure, many studies have been conducted on vessel enhancement. Most studies on vessel enhancement have used Hessian-based methods. These methods use the second-order derivative matrix of the image intensities (Hessian matrix) to detect tubular structures. Among the Hessian-based filters, the most commonly used filter is Frangi’s (4) and the less applied functions are Sato’s (5), Li’s (6), Erdt’s (7), and Zhou’s (8). All these functions can be used to enhance three-dimensional (3D) images. The main advantage of such methods is that they can be performed in a multi-scale manner to detect objects of different sizes. Non-Hessian-based methods have also been investigated. Zeng et al. (9) refined the vessels and highlighted their centers by a combination of oriented flux symmetry and oriented flux anti-symmetry vector measures based on the analysis of directional flux symmetry at the centers and boundaries of the vessels.
From the perspective of theoretical techniques involved in segmentation schemes, coronary artery segmentation methods can be divided into clustering-based methods (10), region growing-based methods (11), active contour model-based methods (12), tracking-based methods (13), and specific theoretical methods (14). Gharleghi et al. have provided a general review on coronary artery segmentation (15). Yi and Ra (16) introduced the method of using local cubes to detect vessel branches based on region growing, and achieved segmentation of several thick blood vessels in the coronary artery. However, the effect is not ideal for thin vessels. Yang et al. (17) developed a hybrid-level set method based on the Bayesian framework for segmenting coronary arteries in CTA images. They used the posterior probability of regional statistical information to construct shape-preserving factors for effective segmentation, but they were unable to segment small parts of coronary arteries with weaker intensity. Cetin et al. (18) defined an intensity-based model to extract coronary arteries from CTA data. The model constructs second-order tensors from image intensity to drive the evolution of vessel segmentation, initializes at a single seed point, and segments the entire vessel tree through an automatic branch detection algorithm. Lee and Lee (19) proposed a semi-automatic segmentation and tracking algorithm for 3D computed tomography (CT) vessels based on the active contour model and Kalman filter. The algorithm performs well in segmentation and tracking by manually selecting a sufficient number of initial points for the active contour model to complete vessel boundary segmentation, and uses a Kalman filter to track the position and shape changes of vessel boundaries between slices. Wang and Jiang (20) combined an implicit 3D vessel model with a level-set method to continuously adjust the vessel centerline and the estimated diameter of the vessel to achieve more accurate vessel segmentation. Besides, the approach by Wang et al. (21) is based on a non-parametric shape-constrained active contour model, which improved the segmentation ability of weak boundaries by adding a shape constraint term to the energy function of the traditional Chan-Vese (CV) active contour model. However, this method is more time-consuming and lacks segmentation ability for small vessels compared to the traditional CV model. In recent years, deep learning-based segmentation methods have received a lot of attention due to their convenient automation and high efficiency. Dong et al. (22) designed a novel multi-attention, multi-scale 3D deep network which addresses the limitation of traditional U-shaped network structures, which often lack the ability to effectively extract contextual information. This new network can synergistically and comprehensively explore core features from multiple perspectives. Zhang et al. (23) proposed a deep learning model for coronary artery segmentation in X-ray angiography images, based on the UNet skeleton. The model incorporates a channel attention module in skip connections and a central auxiliary supervision module at the network’s end. Experiments have demonstrated the effectiveness of these two modules in improving model performance and enabling the network to effectively segment vessels. However, all these methods still suffer from boundary leakage and fail to achieve the desired results, especially in dealing with vessel bifurcations.
In addition, the coronary artery skeleton or centerline provides important pathological information and often plays a crucial role in vessel segmentation. A previous study has shown an overview of available centerline or skeleton extraction techniques (24). Bullitt et al. (25) introduced a ridge detection method to identify centerlines, which utilizes the Hessian value of image intensity. Aylward and Bullitt (26) developed a method based on intensity ridge traversal. The obtained centerline is smoothed using a B-spline-based method. Cui and Xia (27) used an enhanced Frangi filter and calculated the gradient vector field to obtain 3D segmentation results, then used the high-order Runge-Kutta method to calculate the centerline. Overall, accurate coronary artery segmentation still faces challenges. One major challenge is the complex and variable topology of the coronary arteries, which makes it difficult to predict and track the position of the coronary cross section within the slice. Additionally, due to the inhomogeneity intensity of the image, it is arduous to distinguish the coronary arteries from the background objects. To address this issue, this paper proposes a new method for automatic segmentation of coronary arteries based on a local region active contour model. First, an anisotropic diffusion filter is used to remove noise while maintaining vessel boundaries. Then, a two-step strategy is used to extract skeletons for both thick and thin coronary vessels. In the first step of skeleton extraction, clustering is first used to extract the region containing coronary arteries and the heart to remove most of the background objects. Then, an improved Jerman filter is used to enhance this region, and a 3D region growing method that automatically determines seed points is used to extract individual coronary arteries. The skeleton is obtained using thinning methods based on segmentation results. In the second step of the skeleton extraction, based on analyzing the topological structure of the coronary arteries, a cylinder model guided high ridge traversal method is used to obtain the skeleton of thin blood vessels. The final coronary artery skeleton is obtained by merging the skeletons of thick and thin blood vessels to generate the initial contour of the active contour model. Finally, a local region-based geometric active contour model is used for serialized segmentation to obtain the final coronary artery segmentation. A main flowchart of the proposed method is shown in Figure 1. We present this article in accordance with the MDAR reporting checklist (available at https://jtd.amegroups.com/article/view/10.21037/jtd-24-421/rc).
Methods
Preprocessing
To improve the efficiency of subsequent methods, we preprocessed the original images. Preprocessing includes two main steps: window width/level adjustment and noise filtering. The CT volume contains not only the target object, which is the coronary artery, but also other objects such as the ascending aorta and pulmonary vessels, which are within the intensity range of −1,024 to +3,071 Hounsfield unit (HU) in the original CTA images. After the injection of the contrast agent, the HU values of the target objects ranged from 100 to 500. To enhance the contrast between the target objects and the background objects, and to suppress the interference of the neighbouring objects on the target structures, the window width and window level were adjusted on the original CTA images. This changes the range and brightness of each grey level in the image, allowing for mapping adjustments to the grey levels of the image. After this, the image intensity values were normalised to values between 0–255 to remove negative voxels in HU for algorithmic implementation. Since the scattering of X-rays in human tissues during CT imaging or the poor performance of the CT scanning equipment electronics can lead to noisy images, the use of anisotropic diffusion filtering (28) can better preserve the boundaries of the target objects while removing the image noise:
where represents the grayscale level of voxels at time , is the original 3D image, and represent the divergence operator and gradient operator respectively. The conductivity coefficient is a monotonically decreasing function as the image gradient increases, defined as: . The coefficient is the threshold used to control the diffusion rate, which is set as 75 in this paper. The more iterations of filtering, the more obvious the noise filtering effect of the image, but this may affect the clustering effect in the subsequent algorithm. To balance the filtering effect and its impact on subsequent algorithms, we empirically set the number of iterations to 3. The anisotropic diffusion filter was implemented using the Simple Insight Segmentation and Registration Toolkit (SITK), an open-source software widely used in medical image processing. Figure 2 shows the results after processing the image using different number of filtering iterations. The study was conducted in accordance with the Declaration of Helsinki (as revised in 2013).

Vessel skeletonization
Typically, the topology of coronary arteries in CTA images is complex, with thicker portions near the root of the coronary artery and thinner bifurcated vessels away from the root of the coronary artery. These vessels are often surrounded by other objects and share similar intensity, making it difficult to segment individual coronary arteries or to obtain a more complete coronary arterial skeleton via traditional region growing methods. To solve this problem, the skeleton extraction process was divided into two steps and two different strategies were used. Firstly, the thick vessel skeleton closer to the root of the coronary artery was extracted. Then, the thin vessel skeleton of the remaining vessels farther from the coronary root, which could not be extracted in the previous stage, was obtained.
Skeleton extraction of thick vessels
The thick vessel skeletonisation method was first proposed to extract the skeleton of the thicker part of the coronary artery. The process begins by clustering the volumes, followed by extracting the coronary artery through segmentation using the 3D region growing method. Prior to this, the vessels were filtered using a Hessian-based vessel enhancement filter. Lastly, the result from segmentation is skeletonized to finalize the process. In order to reduce the impact of surrounding coronary objects on segmentation and improve the efficiency of subsequent algorithms, we used the K-means clustering method (29) to extract the target object and remove irrelevant objects. After conducting detailed experiments to balance performance and computation time, we set the number of clusters as three.
The three-class clusters correspond visually to the background region, the transition region, and the coronary region (which also contains the heart, some pulmonary vessels, and bone). Based on the vessel prior in the CTA image, the volume of the coronary region is relatively small in the original volume, so we chose the cluster with the smallest number of voxels as the coronary region. The clustering results are shown in Figure 3. In recent years, Jerman et al. (30) proposed a novel vesselness enhancement filter. The filter is briefly described below. This filter is constructed based on a diffusion tensor used to detect approximately spherical structures, which is a metric based on the ratio of eigenvalues:

where are the three eigenvalues of the Hessian matrix, and the eigenvalues are sorted according to their value. In order to detect slender structures (Figure 4A) that satisfy the characteristic of , is used instead of . However, this will suppress the rounded structure (Figure 4B), at which point , will be 0 or close to 0. The term is removed because vessels may often exhibit characteristics of both rounded and tubular structures. As the enhancement function is susceptible to noise, it is difficult to distinguish between local structures when the magnitudes of both with are small, e.g., three eigenvalue magnitudes of a noise voxel with similar magnitudes may be recognised as a rounded structure and be incorrectly enhanced. The regularisation of yield , which increases the difference between eigenvalues at low eigenvalue magnitudes and suppresses the measure of the background structure. At last, the vascular cross-section is more approximated as an ellipse rather than a circle, and is enhanced for the elliptical structure in the filter function. The final proposed filter function for vessels is as follows:

Where is the regularized :
and is a cropping threshold that takes values between 0 and 1. Compared to the Frangi filter, the Jerman filter utilises only two eigenvalues. In order to make full use of the image feature information and at the same time enhance the effect of suppressing the background, this paper proposes to add the background suppression term to the Jerman filter, where is the dimension of the image.
The following improved vesselness filter function is obtained:
Here, the threshold c is taken to be half the value of the maximum Hessian norm. Finally, the optimal vesselness measure values are obtained in combination by calculating the maximum vesselness measure in each scale . The vesselness filtering results are shown in Figure 5, where the new vessel enhancement filtering suppressed some background objects and also enhanced the target object.
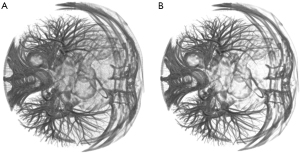
After the vascular enhancement of the image, a 3D region growing method was used to extract the individual coronary arteries. The first step in region growing is to select a set of seed points. The selection of the initial seed point has a direct impact on the result of region growing. In order to avoid the tedious manual selection of seed points, an automatic seed point selection method is proposed. This method uses Hough detection combined with vessel structure prior to the image slices after clustering to obtain the position of the root of the coronary artery in the slice and select the seed point at that position. The coronary arteries begin in the ascending aorta and their roots are connected to the ascending aorta. The ascending aorta is subcylindrical and nearly circular in cross-section, with minimal variation in size between adjacent slices. Due to the similar intensity between the root of the coronary artery and the ascending aorta, the area connecting the coronary artery and the ascending aorta will show an irregular shape in the slice. Hence, the Hough transform (31) was first used to detect the circular in the slices and locate the ascending aorta in the clustered image slices. The circle radius size for Hough circle detection is an important parameter. The radius size of the circle is empirically selected in the range of 35 to 50, and the region of interest (ROI) of the detected image is selected to be a square region centred on the original image, with a side length of 200, to exclude possible false matches. The ascending aorta detection results are shown in Figure 6A. After locating the ascending aorta, the centre of its region is selected as the seed point, and the complete ascending aorta cross-section region is obtained using the flood fill method. Let the number of voxels of the ascending aortic cross-section region be , and the number of voxels of the ascending aortic cross-section region of the next layer of slices be . When , the ascending aorta in the next layer of slices is connected or disconnected from the coronary artery, and is the threshold term, which is set as 0.2 in this paper. Based on the position of the coronary arteries in relation to the ascending aorta, there is a process in the slice where the ascending aortic region connects to the left coronary artery (Figure 6B), then disconnects, and connects to the right coronary artery (Figure 6C) and disconnects again. After detecting the slices where the two connections between the ascending aorta and the coronary artery are located, the coronary root region can be obtained by subtracting the ascending aortic region in the upper slice from the ascending aortic connectivity region, and the centre of this region is selected as the seed voxel to perform the 3D region growing in the filtered image of the blood vessel. If a neighbour voxel of the seed voxel satisfies the similarity criterion, , it is added to the target region and set as a new seed voxel, where is the intensity mean of all the seed voxels, . After clustering, the image was partially removed from the background object and the vessel filtering has further weakened the background object. As a result, the setting in this paper has a larger optional range and can be set to between 0.15 and 0.25, which makes it less prone to over-segmentation. Region growing is terminated when no voxel conforming to the similarity rule is added to the target area. After this step, the thicker coronary arteries are segmented as depicted in Figure 7A. Some of the branches near the end of the coronary has disconnections in the clustering results and are also disconnected after vesselness enhancement filtering.


Due to the intensity inhomogeneity and noise of the image, there are some voxels within the vessels that deviate significantly from the mean vesselness measure within the vascular region, which are difficult to obtain by region growing. For possible holes in the vessels obtained from region growing, close operation is performed on the vessels with the convolution kernel size set to 7×7. The segmented coronary is then skeletonised using the thinning method (32) and the skeleton is shown in Figure 7B.
Skeleton extraction of thin vessels
According to the contrast of the radiocontrast agent, blood can be divided into contrast-enhanced blood, a mixture of unenhanced and enhanced blood (mixed blood), and unenhanced blood (33). The further away from the root of the coronary artery, the smaller the cross-sectional diameter of the vessel. Thick vessels near the root of the coronary artery can be classified as contrast-enhanced blood, whereas thin vessels can be classified as mixed blood. Mixed blood approximates the intensity of the surrounding objects and is thus more difficult to segment compared to thick vessels. To obtain the thin vessel skeleton, the skeleton is extracted using an adaptive threshold height ridge traversal guided by a cylinder model. The vesselness measure at the centre of the vessel is significantly higher than that at the border of the vessel, and these voxels form a ridge of high vesselness measure in the vessel. The greater the vesselness measure of the voxel in the height ridge, the more likely it is to belong to the vessel region. The height ridge traversal method incorporates neighbouring voxels with high vesselness measure into candidate skeleton voxels along one direction starting from a seed voxel (Figure 7C). The coronary artery skeleton is similar to a tree topology. We first found the end nodes from the thick vessel skeleton obtained earlier, which will be referred to as leaf nodes for visual illustration. Leaf nodes in the coronary skeleton have the following characteristics: they have only one skeleton voxel connected to them within a small neighbourhood, and that voxel is positioned away from the coronary root, close to the vessel termination. The leaf node is used as the seed voxel of the height ridge traversal algorithm to track the height ridge along the direction t. For each neighbourhood voxel , its local neighbourhood satisfying with is included as a candidate skeleton voxel. The local neighbourhood size and is the key parameter during candidate skeleton voxel extraction. For example, a smaller and larger local neighbourhood can extract more candidate skeleton voxels, while at the same time leading to the misincorporation of voxels from background regions into the set of candidate voxels. Conversely, a larger is more effective at suppressing background voxels, but may lead to skeleton disconnections. Furthermore, the traversal direction of the height ridge is also crucial. In order to efficaciously extract thick vessel candidate skeleton voxels, we proposed to construct a cylinder model for determining , , and restricting the neighbourhood size to guide the extraction of candidate skeletons, which is inspired by (18). The cylinder model is shown in Figure 7D, and the details are explained as follows.
A sphere centred at the voxel can be denoted as , where is the radius of the sphere. A cylinder with as the center of its base is represented as: , where is the radius of the base circle, is defined as the height of the cylinder, and is the normal vector of the circular base of the cylinder. Next, a set of directional vectors is sampled from the centre of the unit sphere , and each metric in the direction is an image-based feature constructed based on the intensity of the vesselness measure. Formally, the measurement of is expressed as follows:
where is the mean of , and is the mean of , where , . Finally, select , which minimises to , and is used as traverse direction. The height ridge traversal begins at the end of the thick vessels. First, construct an initial sphere with the seed node as the centre. Since the vesselness measure only reaches its maximum value when the Gaussian scale of the filter is consistent with the vessel diameter, can be used to determine the radius of the sphere, i.e., , . The initial threshold value of is the average vessel measure value of voxels in the , which is . In the region of , those that satisfy are selected as candidate skeleton voxels.
During the traversal, the centre of is the intersection of and the circular surface of , and this voxel is used to construct the cylinder model for the next iteration until the terminate condition is satisfied. The mean value of the measure of centred at the current coordinates is and the mean value of the measure of is . If the ratio is less than the given threshold , this indicates that the tracking has reached the end of the vessel and needs to be stopped at the current voxel, which is set to 0.6 in this paper.
After the height ridge traversal, the candidate skeletons are extracted using the thinning algorithm. Due to the low intensity and severe noise, only the skeleton with the largest length is retained as the skeleton for the thick vessels, addressing potential isolated skeletons. Finally, the thick vessel skeleton is merged with the thin vessel skeleton.
Segmentation based on local region geometric active contour model
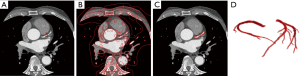
Compared to edge-based active contour models, such as the geodesic active contour (GAC) model (Figure 8A) (34) and the distance regularized level set evolution (DRLSE) model (35), region-based geometric active contour models can deal with boundary leakage and intensity inhomogeneities more effectively (36). Local region geometric active contour model such as region-scalable fitting (RSF) model (37) is suitable for two-phase image segmentation, and the definition of the energy function is based on a single voxel. Even at locations far from the initial contour, the contour appears quickly in these regions after a few iterations. These models often segment the entire image (Figure 8B), making it difficult to detect a single target from a complex background. The CV model (38) differs from the aforementioned models, in that its energy function is defined based on the whole image, and its contour does not evolve too quickly, allowing its utilisation for the segmentation of small targets (Figure 8C).
Compared to the CV model, the Localised Chan-Vese (LCV) model (39) is based on fitting the intensity to a local region and is more robust to intensity inhomogeneity in the image. Hence, we applied the LCV model to coronary segmentation. Given that the segmentation target usually occupies a small area in the image, it is difficult to segment the target object solely based on intensity. Here, we used , which integrates image intensity and vesselness measure, to replace the intensity-based measurement, i.e., in the original LCV model, where is a weight factor that balances intensity values and vesselness measurement, set to 0.8 in this paper.
At the same time, in order to avoid re-initialisation of the level set function and to improve the stability of the model evolution, the regular term of the level set function in DRLSE is added to the energy function:
where is a double-well potential function that keeps the signed distance property, , in regions adjacent to the zero level set, and keeps the level-set function (LSF) as a constant, , away from the zero level set, thereby reducing irregularities in the evolution of the LSF.
Using the zero-level set of a Lipschitz function to represent the curve, the entire energy functional can be expressed as:
where the length term coefficient is represented by , the closed contour is denoted by and the image domain by . Additionally, and represent the mean values of the fitted intensity of the local regions of the image:
The given Eqs. [9] and [10] includes the smoothed Heaviside function and the Dirac function respectively. is a characteristic function in terms of a radius parameter , and we use to mask local regions.
According to the continuous gradient descent flow method, the partial differential equation (PDE) of the evolution contour is expressed as:
where and are weight coefficients. For the proposed model, it is sensitive to initialization, and the initial contour is generated using the previously obtained coronary skeleton for serialization segmentation. The skeleton is generally represented as one or several small connected areas in the slice. In order to balance model performance and computation cost, the voxel at the centre of the connected area is selected to generate a 3×3 rectangle as the initial contour of the active contour model. Due to the excellence of the initial contour, we could obtain fast convergence of the LSF. Figure 8D shows the results of the final segmentation using the active contour model. We found that the proposed method can efficiently segment almost all thick vessels and avoid severe over-segmentation and under-segmentation. In addition, our method also maintained a certain degree of smoothness on the vessel surface and preserved the continuity of the vessel shape. However, some terminal vessels were not segmented due to their low intensities.
Results
As an illustration of the validity of the methods in this paper, we applied them to validate the Automated Segmentation of Coronary Arteries (ASOCA) challenge dataset (40). The dataset comprises of 40 training and 20 test cases, including both normal and diseased patients. The experiments were performed via Python and the MATLAB R2017b platform on a computer equipped with an Intel Core i5 1.6 GHz CPU with 16 GB of RAM.
For clinical CTA images, the detailed parameters are set to the default values listed in the Methods section. Figure 9 shows the segmentation results of five different original CTA images and their corresponding methods of the previous study (41), the CV model and the method proposed in this paper. In order to make the comparison as fair as possible, the parameters in the previous study (41) and the CV model were optimized to obtain the best segmentation results. It is observed that, compared to the segmentation obtained by the method in the previous study (41) and CV model, the proposed method can segment more thick blood vessels despite the weak boundary and low contrast between the thick blood vessels and cardiac tissues. This is mainly attributed to our method extracting a more complete coronary skeleton, which provides a good guide for the segmentation of the active contour model. Even if the segmentation of the middle part of the slice fails, it does not affect the segmentation of the other slices. Furthermore, our method effectively utilizes vessel intensity and local structural information, and is better able to handle regions with intensity inhomogeneity and segment thick vessels more accurately than the other two methods from the use of an active contour model based on local region.

In order to quantify the segmentation performance of the method, three commonly used evaluation measures: precision, recall, and dice similarity coefficient (DSC), are used in this paper. These measures are defined as follows:
where TP, FP and FN denote true positives (the number of vessel voxels correctly identified), false positives (the number of non-vessel voxels incorrectly identified as vessel voxels), and false negatives (the number of vessel voxels that are not identified as vessel voxels), respectively. The DSC ranges from 0 to 1, with 1 denoting complete overlap.
Table 1 shows the segmentation performance of the other four different methods compared to our method on the twenty CTA datasets. Among them, the CV method and the method in the study of (41) are our implementations in this dataset, and the metric values of UNet (42) and VNet (43) methods are derived from studies in the same dataset in reference (44). We can find that the average segmentation accuracy, recall, and DSC of this method are 86.64%, 91.26%, and 79.13%, respectively. Our method scored the highest in precision and recall, and was on par with the VNet method in DSC. Considering the current superiority of VNet in deep learning-based methods, we believe that the performance of our method is acceptable.
Table 1
| Methods | Precision | Recall | DSC |
|---|---|---|---|
| Jawaid et al. (41) | 0.8022±0.0607 | 0.8290±0.0941 | 0.7408±0.0698 |
| CV (38) | 0.7765±0.0552 | 0.7286±0.1039 | 0.6832±0.1064 |
| UNet (42) | 0.748±0.08 | 0.837±0.10 | 0.787±0.06 |
| VNet (43) | 0.759±0.06 | 0.849±0.08 | 0.806±0.08 |
| Our method | 0.8664±0.0734 | 0.9126±0.0720 | 0.7913±0.0815 |
The indicator value is expressed in the form of mean ± SD. DSC, dice similarity coefficient; CV, Chan-Vese active contour model; SD, standard deviation.
To further demonstrate the impact of the skeleton and vessel measure features on the segmentation performance of the method, an example is given to illustrate it for the following two different cases: (A) the proposed method does not use a skeleton to help generate the initial contour of the active contour model (we use the centroid of the area of the segmentation result of the previous slice to set the initialization in the next slice); and (B) the active contour model in the proposed method works without information of vesselness measure.
Figure 10A shows the results of coronary artery segmentation in case A. It is observed that the thick vessels can be segmented effectively, but fail to segment some of the thin vessels effectively. This is mainly due to the complex topology of the vessels, which often appear far away from the segmentation area in the last slice, and when there is a lack of positional guidance for these vessels, active contour model cannot segment without producing over-segmentation. Figure 10B gives the segmentation for case B. The segmentation of thick vessels performs well, but thin vessels cannot be segmented due to low intensity, resulting in over-segmentation, and the failure to segment this slice resulted in the production of disconnected vessels. The segmentation of the method of this paper is shown in Figure 10C, which uses the skeleton to obtain information about the overall topology of the coronary arteries. Since the vesselness measure are integrated into the energy function of the active contour model (see Eq. [13]), both thin and thick vessels are efficiently segmented compared to the segmentation results of cases A and B.

However, there are drawbacks in the proposed method. For example, it failed to segment the thin vessels that were not extracted from the skeleton, and part of the thin blood vessels that were extracted to the skeleton had disconnections (see Figure 10C). This is mainly attributed to the local-region-based active contour model driving the evolution of the contour based on the intensity differences between the inner and outer regions of the contour, and its tendency to segment vessels with larger intensity and vesselness measure. When the contrast between thin vessels and surrounding objects is low, over-segmentation may occur due to misclassification of vessel voxels with lower intensity into the foreground, or under-segmentation may occur due to misclassification of vessel voxels with higher intensity into background objects, resulting in the failed segmentation of the slice.
Discussion
In this paper, we developed a coronary segmentation method based on the local region active contour model. In general, effective segmentation of thin and thick vessels is quite difficult due to inhomogeneities in intensity, severe noise, and low contrast. For example, GAC rely on gradient information to segment blood vessels, which can easily lead to over-segmentation. Graph-cut-based methods usually encounter the problem of structural contraction bias in elongated vessels, and the same problem occurs in level-set-based methods. In fact, due to the complex geometric topology and intensity distribution, it is difficult to obtain good segmentation results using the active contour model alone, e.g., coronary arteries in different slices may be far away from each other, and sometimes some coronary arteries may suddenly appear in one location in one slice and disappear in the next slice, so it is necessary to consider other methods to assist segmentation using the active contour model. Based on this idea, we applied two different strategies to extract the skeleton of thin and thick vessels and used the skeleton to guide the segmentation of the active contour model. The proposed active contour model utilizes the overall topological information of the coronary artery represented by the coronary artery skeleton with the local structural a priori of the vessel provided by the vesselness measure values integrated into the energy function. In order to extract the skeleton of thick vessels, K-means cluster was first used to remove most of the background objects. The improved Jerman vesselness filter was applied to enhance the suppression ability of background objects and improve the efficiency of subsequent algorithms. Then, the 3D region growing method was used to extract individual coronary arteries that do not include the ascending aorta. Compared to the direct extraction of the coronary skeleton using a 3D region growing method, the clustered image removed a large number of background voxels while preserving the vessel branches, even though some of the thin-vessel branches were disconnected, which still provided the subsequent algorithms with critical information about the branch initiation location. In the thin vessel skeleton extraction step, candidate skeleton voxels were obtained using a height ridge traversal method. To improve the robustness of the algorithm, a cylinder model was used to guide the traversal and automatically determine the parameters , and neighbourhood range. Lastly, the thin vessel skeleton and the thick vessel skeleton were merged to form the final coronary skeleton, which was used in the active contour model to generate the initial contour. The skeleton voxels marked the location of almost all vessels within the section, and the active contour model did not miss the segmentation of these vessels. Moreover, as the energy function of local region active contour models, such as the RSF model, is defined based on voxels, it performs a two-phase segmentation of the image. This often results in the entire heart being segmented as the foreground and the lungs as the background due to the high contrast between the cardiac and lung region, making it difficult to segment the coronary surrounded by the cardiac tissue in the image slices. To solve this problem, we selected the LCV model, which defines the energy function based on the whole image as the segmentation model. The method has been evaluated on a public CTA dataset, and the experimental results showed that the method can segment coronary arteries effectively with precision, recall and DSC of 86.64%, 91.26% and 79.13%, respectively. Additionally, our method can segment thinner vessels compared to the other two methods as mentioned above. In conclusion, the good performance of the method is mainly attributed to the efficient extraction of the vessel skeleton using a two-step approach and the ability to accurately drive the convergence of the active contours to the vessel boundaries by introducing information about the vesselness measure into the local region active contour model.
Due to differences in imaging quality among different CT machines, the method proposed in this paper may not achieve ideal segmentation when CT imaging quality is poor. For example, due to individual differences in coronary artery structure and the fluidity of contrast agents in the coronary artery, some images may have lower contrast between the coronary artery and surrounding tissues. In this case, the window width and level can be adjusted appropriately to perform grayscale mapping on the image and increase its contrast. If there is a lot of image noise, the local region active contour model cannot accurately fit the local intensity, and it is more prone to falling into local optima and segmentation failure during the segmentation process, that is, the contour curve after evolution convergence spreads outside the coronary area or contracts into a point. At this point, the number of iterations of anisotropic diffusion filtering can be appropriately increased to enhance the noise filtering effect and achieve the desired segmentation effect. However, it should be noted that excessive smoothing of the image may lead to poor clustering performance and blurred edges. When the active contour model fails to segment the slices, it can cause the 3D reconstructed coronary artery to break, and most of the time, these breaks occur at the distal portion of the coronary artery. Clinicians should pay attention to these broken areas and the unsegmented vessels at the terminal. They can perceive their positions based on the continuity of vessel positions and the intensity between adjacent slices, and observe these slices layer by layer in the CT image.
Strengths, limitations and future works
The method in this article combines the advantages of multiple algorithms and proposes to use an improved Jerman vascular enhancement filter and cylindrical model to guide the extraction of candidate skeletons in the process of extracting coronary artery skeletons using a two-step method, achieving a relatively complete extraction of coronary artery skeletons. The active contour model can incorporate prior terms into the energy function of the model based on the features of the image, allowing the model to fully integrate image characteristics for segmentation. The local region active contour model has stronger adaptability to features of intensity inhomogeneity and strong noise in medical images. By incorporating vesselness measure into the local region fitting term, the model can utilize the local geometric structure information of the image. Meanwhile, using the coronary skeleton to initialize the initial contour of the active contour model enables the model to grasp the global topological structure information of the coronary artery. Therefore, this method fully adapts to the characteristics of CTA images and utilizes slice context information, grasping the geometric topology information of coronary arteries globally and locally, ultimately achieving good segmentation results. Finally, the method proposed in this paper does not require a tedious training process, nor does it require manual selection of seed points and initial contours, making it relatively easy to use.
However, there are still some limitations in our current research. Firstly, the dataset used in this study has a relatively small sample size, and the generalization performance of this method still needs to be validated on larger scale datasets. Secondly, there were disconnections in some of the segmented vessels and some of the thin vessels with low intensity could not be segmented, which is a common problem with other segmentation methods. Thirdly, although the images were first filtered using a nonlinear anisotropic diffusion filter, the surface of the coronary arteries segmented by our method was not very smooth. Fourthly, the algorithm in this paper took approximately 15 minutes to segment a typical volume of size 512×512×275, and most of the running time was spent on active contour model segmentation, which was significantly longer than the computation time of the methods in the study of (41).
In future work, considering the unique advantages of deep learning, we will attempt to combine local region active contour models with deep learning models, such as (I) exploring a segmentation framework from coarse to fine, using segmentation based on deep learning models as coarse segmentation, and then refining the segmentation results using active contour models; (II) incorporating the segmentation of active contour models into the training process of deep learning models to enhance their feature extraction capabilities. By exploring the potential of applying local region active contour models in coronary artery segmentation, we hope to obtain a more high-performance coronary artery segmentation model and attempt to validate it on large-scale datasets.
Conclusions
In this paper, we proposed an effective coronary segmentation method based on a local region active contour model. Due to the low contrast, severe noise, and inhomogeneities in intensity between thin and thick vessels in the coronary vessels in CTA images, two strategies were used to extract the skeleton for thick and thin coronary vessels. The overall topological information of the coronary artery characterised by the skeleton was then used for effective segmentation using the active contour model with the local structural a priori of the vessels provided by the vesselness measure integrated into the active contour model. For thick vessels, the images were first clustered, after which the thick vessels were extracted using a 3D region growing method after vessel enhancement using a modified Jerman vesselness enhancement filter. For the thin vessels, candidate skeletal voxels were obtained using a height ridge traversal approach and a cylinder model to guide the traversal and automatically determine the threshold parameter, traversal direction and neighbourhood range. The vessel skeleton was generated using a thinning method on the segmentation results. Lastly, the thick and thin vessel skeletons were merged as the final skeleton to guide the segmentation based on the active contour model. To address the intensity inhomogeneity of the image, a priori information about the local structure of the vessel characterised by the vesselness measure was introduced into the active contour model, and the coronary was finally segmented. The method does not rely on manual selection of seed points with initial contours and avoids the heavy training process as in the case of deep learning-based methods. Experiments on the public dataset of coronary CTA showed that our method has better segmentation than other 3D vessel segmentation methods in terms of precision, recall, and DSC. Moreover, our method allows for accurate segmentation of thick vessels by exploiting information about the intensity and vesselness measure values. Meanwhile, the segmentation results of our method contain more thin vessels. Although some of them appear to have blurred and disconnected boundaries, radiologists can perceive them based on the continuity of the vessel location and the intensity between neighbouring slices, which are difficult to segment using conventional algorithms. At last, our proposed automatic coronary artery segmentation algorithm is expected to be applied in medical teaching, clinical trials, and assisting conventional clinical diagnosis.
Acknowledgments
Funding: None.
Footnote
Reporting Checklist: The authors have completed the MDAR reporting checklist. Available at https://jtd.amegroups.com/article/view/10.21037/jtd-24-421/rc
Peer Review File: Available at https://jtd.amegroups.com/article/view/10.21037/jtd-24-421/prf
Conflicts of Interest: All authors have completed the ICMJE uniform disclosure form (available at https://jtd.amegroups.com/article/view/10.21037/jtd-24-421/coif). The authors have no conflicts of interest to declare.
Ethical Statement: The authors are accountable for all aspects of the work in ensuring that questions related to the accuracy or integrity of any part of the work are appropriately investigated and resolved. The study was conducted in accordance with the Declaration of Helsinki (as revised in 2013).
Open Access Statement: This is an Open Access article distributed in accordance with the Creative Commons Attribution-NonCommercial-NoDerivs 4.0 International License (CC BY-NC-ND 4.0), which permits the non-commercial replication and distribution of the article with the strict proviso that no changes or edits are made and the original work is properly cited (including links to both the formal publication through the relevant DOI and the license). See: https://creativecommons.org/licenses/by-nc-nd/4.0/.
References
- Sleeman KE, de Brito M, Etkind S, et al. The escalating global burden of serious health-related suffering: projections to 2060 by world regions, age groups, and health conditions. Lancet Glob Health 2019;7:e883-92. [Crossref] [PubMed]
- GBD 2013 Mortality and Causes of Death Collaborators. Global, regional, and national age-sex specific all-cause and cause-specific mortality for 240 causes of death, 1990-2013: a systematic analysis for the Global Burden of Disease Study 2013. Lancet 2015;385:117-71. [Crossref] [PubMed]
- Xiao C, Staring M, Shamonin D, et al. A strain energy filter for 3D vessel enhancement with application to pulmonary CT images. Med Image Anal 2011;15:112-24. [Crossref] [PubMed]
- Frangi AF, Niessen WJ, Vincken KL, et al. Multiscale vessel enhancement filtering. Medical Image Computing and Computer-Assisted Intervention — MICCAI’98: First International Conference Cambridge; 1998;130-7.
- Sato Y, Westin C, Bhalerao A, et al. Tissue classification based on 3d local intensity structures for volume rendering. IEEE Trans Vis Comput Graph 2000;6:160-80. [Crossref]
- Li Q, Sone S, Doi K. Selective enhancement filters for nodules, vessels, and airway walls in two- and three-dimensional CT scans. Med Phys 2003;30:2040-51. [Crossref] [PubMed]
- Erdt M, Raspe M, Suehling M. Automatic hepatic vessel segmentation using graphics hardware. In: Medical Imaging and Augmented Reality: 4th International Workshop Tokyo, Japan; August 1-2, 2008:403-12.
- Zhou C, Chan HP, Sahiner B, et al. Automatic multiscale enhancement and segmentation of pulmonary vessels in CT pulmonary angiography images for CAD applications. Med Phys 2007;34:4567-77. [Crossref] [PubMed]
- Zeng YZ, Zhao YQ, Tang P, et al. Liver vessel segmentation and identification based on oriented flux symmetry and graph cuts. Comput Methods Programs Biomed 2017;150:31-9. [Crossref] [PubMed]
- Thanapong C, Watcharachai W, Somporn R, et al. Extraction Blood Vessels from Retinal Fundus Image Based on Fuzzy C-Median Clustering Algorithm. Fourth International Conference on Fuzzy Systems and Knowledge Discovery (FSKD 2007), Haikou, China; 2007:144-8.
- Kerkeni A, Benabdallah A, Manzanera A, et al. A coronary artery segmentation method based on multiscale analysis and region growing. Comput Med Imaging Graph 2016;48:49-61. [Crossref] [PubMed]
- Yang Y, Hou X, Ren H. Efficient active contour model for medical image segmentation and correction based on edge and region information. Expert Syst Appl 2022;194:116436. [Crossref]
- Zhou C, Chan HP, Chughtai A, et al. Automated coronary artery tree extraction in coronary CT angiography using a multiscale enhancement and dynamic balloon tracking (MSCAR-DBT) method. Comput Med Imaging Graph 2012;36:1-10. [Crossref] [PubMed]
- Du H, Shao K, Bao F, et al. Automated coronary artery tree segmentation in coronary CTA using a multiobjective clustering and toroidal model-guided tracking method. Comput Methods Programs Biomed 2021;199:105908. [Crossref] [PubMed]
- Gharleghi R, Chen N, Sowmya A, et al. Towards automated coronary artery segmentation: A systematic review. Comput Methods Programs Biomed 2022;225:107015. [Crossref] [PubMed]
- Yi J, Ra JB. A locally adaptive region growing algorithm for vascular segmentation. Int J Imaging Syst Technol 2003;13:208-14. [Crossref]
- Yang Y, Tannenbaum A, Giddens D, et al. Automatic segmentation of coronary arteries using bayesian driven implicit surfaces. Proceedings of the 4th IEEE International Symposium on Biomedical Imaging: From Nano to Macro (ISBI '07); April 2007:189-92.
- Cetin S, Demir A, Yezzi A, et al. Vessel tractography using an intensity based tensor model with branch detection. IEEE Trans Med Imaging 2013;32:348-63. [Crossref] [PubMed]
- Lee SH, Lee S. Adaptive Kalman snake for semi-autonomous 3D vessel tracking. Comput Methods Programs Biomed 2015;122:56-75. [Crossref] [PubMed]
- Wang Y, Jiang H. A nonparametric shape prior constrained active contour model for segmentation of coronaries in CTA images. Comput Math Methods Med 2014;2014:302805. [Crossref] [PubMed]
- Wang C, Moreno R, Smedby Ö. Vessel segmentation using implicit model-guided level sets. In MICCAI Workshop. 3D Cardiovascular Imaging: a MICCAI segmentation Challenge workshop. Nice, France; 1st of October 2012.
- Dong C, Xu S, Dai D, et al. A novel multi-attention, multi-scale 3D deep network for coronary artery segmentation. Med Image Anal 2023;85:102745. [Crossref] [PubMed]
- Zhang Y, Gao Y, Zhou G, et al. Centerline-supervision multi-task learning network for coronary angiography segmentation. Biomed Signal Process Control 2023;82:104510. [Crossref]
- Cornea N, Silver D, Min P. Curve-skeleton applications. In: VIS 05. IEEE Visualization; 2005:95-102.
- Bullitt E, Aylward S, Smith K, et al. Symbolic description of intracerebral vessels segmented from magnetic resonance angiograms and evaluation by comparison with X-ray angiograms. Med Image Anal 2001;5:157-69. [Crossref] [PubMed]
- Aylward SR, Bullitt E. Initialization, noise, singularities, and scale in height ridge traversal for tubular object centerline extraction. IEEE Trans Med Imaging 2002;21:61-75. [Crossref] [PubMed]
- Cui H, Xia Y. Automatic coronary centerline extraction using gradient vector flow field and fast marching method from CT images. IEEE Access 2018;6:41816-26.
- Perona P, Malik J. Scale-space and edge detection using anisotropic diffusion. IEEE Trans Pattern Anal Mach Intell 1990;12:629-39. [Crossref]
- Lee E, Schmidt M, Wright J. Improved and simplified inapproximability for k-means. Information Processing Letters 2017;120:40-3. [Crossref]
- Jerman T, Pernuš F, Likar B, et al. Beyond Frangi: an improved multiscale vesselness filter. Proc. SPIE 9413, Medical Imaging 2015 Image Processing 2015;9413:623-33.
- Duda RO, Hart PE. Use of the Hough transformation to detect lines and curves in pictures. Commun ACM 1972;15:11-5. [Crossref]
- Ma CM. On topology preservation in 3D thinning. CVGIP: Image Understanding 1994;59:328-39. [Crossref]
- Scholtz JE, Ghoshhajra B. Advances in cardiac CT contrast injection and acquisition protocols. Cardiovasc Diagn Ther 2017;7:439-51. [Crossref] [PubMed]
- Caselles V, Kimmel R, Sapiro G. Geodesic active contours. Int J Comput Vis 1997;22:61-79. [Crossref]
- Li C, Xu C, Gui C, et al. Distance regularized level set evolution and its application to image segmentation. IEEE Trans Image Process 2010;19:3243-54. [Crossref] [PubMed]
- Yan Zhang Y, Matuszewski BJ, Shark LK, et al. Medical image segmentation using new hybrid level-set method. In: 2008 fifth international conference biomedical visualization: information visualization in medical and biomedical informatics; 2008;12:71-6.
- Li C, Kao CY, Gore JC, et al. Minimization of region-scalable fitting energy for image segmentation. IEEE Trans Image Process 2008;17:1940-9. [Crossref] [PubMed]
- Chan TF, Vese LA. Active contours without edges. IEEE Trans Image Process 2001;10:266-77. [Crossref] [PubMed]
- Lankton S, Tannenbaum A. Localizing region-based active contours. IEEE Trans Image Process 2008;17:2029-39. [Crossref] [PubMed]
- Gharleghi R, Adikari D, Ellenberger K, et al. Automated segmentation of normal and diseased coronary arteries - The ASOCA challenge. Comput Med Imaging Graph 2022;97:102049. [Crossref] [PubMed]
- Jawaid MM, Rajani R, Liatsis P, et al. A hybrid energy model for region based curve evolution - Application to CTA coronary segmentation. Comput Methods Programs Biomed 2017;144:189-202. [Crossref] [PubMed]
- Ronneberger O, Fischer P, Brox T. U-Net: Convolutional networks for biomedical image segmentation. Medical image computing and computer-assisted intervention–MICCAI 2015:18th international conference, Munich, Germany, October 5-9, proceedings, part III 18. Springer International Publishing; 2015;234-41.
- Milletari F, Navab N, Ahmadi SA. V-net: Fully convolutional neural networks for volumetric medical image segmentation. 2016 fourth international conference on 3D vision (3DV). IEEE 2016:565-71.
- Qiu Y, Chai S, Zhu E, et al. Deep multi-scale dilated convolution network for coronary artery segmentation. Biomed Signal Process Control 2024;92:106021. [Crossref]



